Bem-vindo ao nosso espaço dedicado aos exercícios de correlação linear e regressão linear! Esses dois conceitos são fundamentais no estudo de dados e aparecem em várias situações do cotidiano escolar, científico e profissional.
Nesta seção, você encontrará uma variedade de exercícios práticos elaborados especialmente para ajudá-lo a compreender e aplicar os principais conceitos da regressão linear e da correlação entre variáveis. Aqui, você poderá praticar como encontrar a equação da reta de regressão, calcular o coeficiente de correlação linear, determinar variâncias, covariâncias e muito mais.
Vamos começar a explorar o fascinante universo das relações estatísticas e entender, passo a passo, como os dados se comportam, tornando você cada vez mais confiante nesses conteúdos!
Uma empresa deseja fazer previsões sobre o valor anual de suas vendas totais em determinado país, a partir da relação entre essas vendas e a renda nacional. Para investigar essa relação, a empresa dispõe dos seguintes dados:
X representa a renda nacional em milhões de reais e Y representa as vendas da empresa em milhares de reais, no período de  a
a  (inclusive).
(inclusive).
Calcule:
1. A reta de regressão de Y sobre X.
2. O coeficiente de correlação linear e interpretá-lo.
3. Em 2001, a renda nacional do país foi de R$325 milhões de reais. Qual será a previsão para as vendas da empresa nesse ano?
Uma empresa deseja fazer previsões sobre o valor anual de suas vendas totais em determinado país, a partir da relação entre essas vendas e a renda nacional. Para investigar essa relação, a empresa dispõe dos seguintes dados:

X representa a renda nacional em milhões de reais e Y representa as vendas da empresa em milhares de reais, no período de  a
a  (inclusive).
(inclusive).
Calcule:
1 A reta de regressão de Y sobre X.









2 O coeficiente de correlação linear e interpretá-lo.

É um coeficiente de correlação positivo e próximo de um, portanto a correlação é direta e forte.
3 Se, em 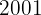 , a renda nacional do país foi de R$
, a renda nacional do país foi de R$  milhões de reais, qual será a previsão para as vendas da empresa nesse ano?
milhões de reais, qual será a previsão para as vendas da empresa nesse ano?

A informação estatística obtida de uma amostra de tamanho 12 sobre a relação existente entre o investimento realizado e o rendimento obtido, em centenas de milhares de euros, para explorações agrícolas, é apresentada no quadro a seguir: Investimento (X), Rendimento (Y).

Calcule:
1 A reta de regressão do rendimento em função do investimento.
2 A previsão do investimento necessário para obter um rendimento de R$ 1.250.000.
A informação estatística obtida de uma amostra de tamanho 12 sobre a relação existente entre o investimento realizado e o rendimento obtido, em centenas de milhares de euros, para explorações agrícolas, é apresentada no quadro a seguir:

Calcule:
1 A reta de regressão do rendimento em função do investimento.





2 A previsão do investimento necessário para obter um rendimento de R$ 1.250.000.


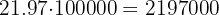
O número de horas dedicadas ao estudo de uma disciplina e a nota obtida na prova correspondente, por oito pessoas, é o seguinte: Horas (X) — Nota (Y)

Pede-se:
1 A reta de regressão de Y em função de X.
2 A nota estimada para uma pessoa que tenha estudado  horas.
horas.
O número de horas dedicadas ao estudo de uma disciplina e a nota obtida na prova correspondente, por oito pessoas, é o seguinte:

Pede-se:
1 A reta de regressão de Y em função de X.
 ]
]






2 A nota estimada para uma pessoa que tenha estudado  horas.
horas.

Na tabela seguinte são apresentadas a idade (em anos) e a conduta agressiva (medida em uma escala de zero a 10) de 10 crianças.
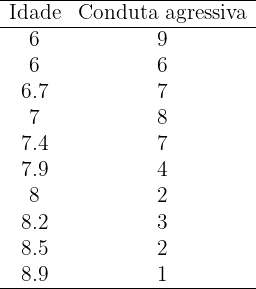
1 Obter a reta de regressão da conduta agressiva em função da idade.
2 A partir dessa reta, obter o valor da conduta agressiva que corresponderia a uma criança de  anos.
anos.
Na tabela seguinte são apresentadas a idade (em anos) e a conduta agressiva (medida em uma escala de zero a 10) de 10 crianças.

1 Obter a reta de regressão da conduta agressiva em função da idade.







2 A partir dessa reta, obter o valor da conduta agressiva que corresponderia a uma criança de  anos.
anos.

Os valores de duas variáveis X e Y se distribuem conforme a tabela a seguir:

Pede-se:
1 Calcular a covariância.
2 Obter e interpretar o coeficiente de correlação linear.
3 Determinar a equação da reta de regressão de Y sobre X.
Os valores de duas variáveis X e Y se distribuem conforme a tabela a seguir:

Pede-se:
1 Calcular a covariância.
Vamos converter a tabela de dupla entrada em uma tabela simples.








2 Obter e interpretar o coeficiente de correlação linear.

É uma correlação negativa fraca.
3 Determinar a equação da reta de regressão de Y sobre X.

As pontuações obtidas por um grupo de alunos em uma bateria de testes que mede a habilidade verbal (X) e o raciocínio abstrato (Y) são as seguintes:

Pede-se:
1 Existe correlação entre as duas variáveis?
2De acordo com os dados da tabela, se um desses alunos obtiver uma pontuação de  pontos em raciocínio abstrato, qual será a estimativa para sua habilidade verbal?
pontos em raciocínio abstrato, qual será a estimativa para sua habilidade verbal?
As pontuações obtidas por um grupo de alunos em uma bateria de testes que mede a habilidade verbal (X) e o raciocínio abstrato (Y) são as seguintes:

Pede-se
1 Existe correlação entre as duas variáveis?
Transformamos a tabela de dupla entrada em uma tabela simples.









Existe uma correlação positiva forte.
2 De acordo com os dados da tabela, se um desses alunos obtiver uma pontuação de  pontos em raciocínio abstrato, em quanto será estimada sua habilidade verbal?
pontos em raciocínio abstrato, em quanto será estimada sua habilidade verbal?


Sabe-se que entre o consumo de papel e o número de litros de água por metro quadrado que são recolhidos em uma cidade não existe relação.
1 Qual é o valor da covariância dessas variáveis?
2 Quanto vale o coeficiente de correlação linear?
3 Quais são as equações das duas retas de regressão e qual é a sua posição no plano?
Sabe-se que entre o consumo de papel e o número de litros de água por metro quadrado recolhidos em uma cidade não existe relação.
1 Qual é o valor da covariância dessas variáveis?

2 Quanto vale o coeficiente de correlação linear?

3 Quais são as equações das duas retas de regressão e qual é a sua posição no plano?

As retas são paralelas aos eixos coordenados e perpendiculares entre si.
Em uma empresa de transportes trabalham quatro motoristas. Os anos de habilitação (tempo de posse da carteira de motorista) e o número de infrações cometidas por cada um deles no último ano são os seguintes:
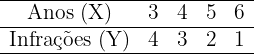
Calcule o coeficiente de correlação linear e interprete o resultado.
Em uma empresa de transportes trabalham quatro motoristas. Os anos de habilitação (tempo de posse da carteira de motorista) e o número de infrações cometidas por cada um deles no último ano são os seguintes:
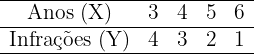
Calcule o coeficiente de correlação linear e interprete o resultado.



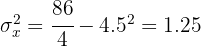



A correlação é perfeita e inversa.
Uma pessoa faz semanalmente a Lotofácil e também aposta na Mega-Sena, anotando o número de acertos que obtém em cada uma. Durante as quatro semanas do mês de fevereiro, os acertos foram:
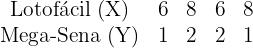
Obtenha o coeficiente de correlação linear e interprete o resultado. As previsões feitas pelas retas de regressão seriam confiáveis?
Uma pessoa faz semanalmente a Lotofácil e também aposta na Mega-Sena, anotando o número de acertos que obtém em cada uma. Durante as quatro semanas do mês de fevereiro, os acertos foram:
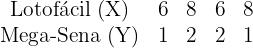
Obtenha o coeficiente de correlação linear e interprete o resultado. As previsões feitas pelas retas de regressão seriam confiáveis?









Não existe correlação entre as duas variáveis, portanto as estimativas feitas com as retas de regressão não oferecem qualquer confiança.
Temos uma tabela que relaciona duas variáveis da seguinte forma:

Pede-se:
1 Encontre a covariância e o desvio-padrão.
2 Encontre o coeficiente de correlação linear.
Temos uma tabela que relaciona duas variáveis da seguinte forma:

Pede-se:
1 Encontre a covariância e o desvio-padrão.

Então, o desvio-padrão de cada variável é:

e a a covariância é:

2 Encontre o coeficiente de correlação linear.

Ou seja, há uma correlação inversa fraca.


