Bem-vindos à nossa página: onde integrais e cálculo de áreas ganham vida! Já se perguntou como medir superfícies curvas ou irregulares usando matemática avançada? Aqui, você vai aprender como usar integrais para calcular áreas de formas complexas: desde áreas simples sobre gráficos de funções até formas curvas mais elaboradas.
Com exemplos práticos e didáticos, vamos juntos explorar como aplicar as integrais no mundo real. Prepare-se para expandir seus conhecimentos e enxergar a beleza por trás das contas!
Aventure-se nesse universo fascinante e domine o cálculo de áreas com integrais. Vamos começar?
Encontre a área limitada pela reta  , o eixo
, o eixo  e as retas
e as retas  y
y 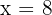 .
.
a. Vamos fazer a representação gráfica das retas e do eixo indicados no enunciado e destacar a área solicitada.
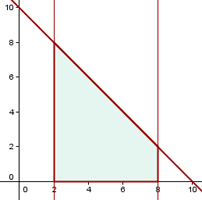
b. Os limites da área solicitada são definidos pelas retas  e
e 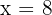 . Por isso, representamos a reta em função da variável
. Por isso, representamos a reta em função da variável 
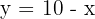
c. A área solicitada é determinada por:

d. Substituimos  em função de
em função de  e resolvemos a integral definida:
e resolvemos a integral definida:

Calcule a área delimitada pela curva 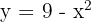 e pelo eixo
e pelo eixo  .
.
a. Encontre os pontos de interseção com o eixo  , tendo em consideração que esses serão os limites de integração. Por isso, igualamos a curva a zero e encontramos os valores de
, tendo em consideração que esses serão os limites de integração. Por isso, igualamos a curva a zero e encontramos os valores de 
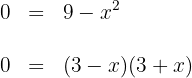
Sendo assim, 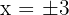 são os pontos onde a curva corta o eixo
são os pontos onde a curva corta o eixo  , conforme a representação gráfica a seguir:
, conforme a representação gráfica a seguir:
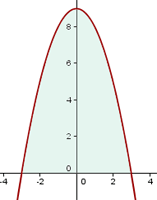
b. A área solicitada é:
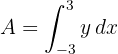
c. Substituímos  em função de
em função de  e resolvemos a integral:
e resolvemos a integral:

Como a parábola é simétrica em relação ao eixo 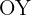 , a área será igual ao dobro da área comprendida entre
, a área será igual ao dobro da área comprendida entre 

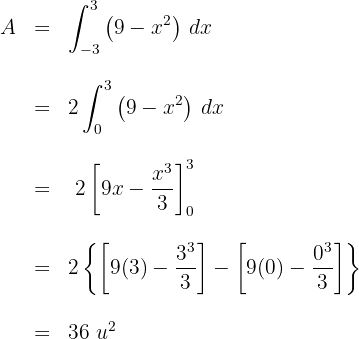
Calcule a área do triángulo de vértices 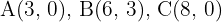 .
.
a. Vamos começar fazendo um gráfico dos pontos dados e destacar a área
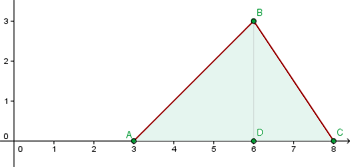
b. Calculamos as inclinações das retas  e
e  para determinar suas equações.
para determinar suas equações.

c. A área solicitada está dividida em duas partes, uma para cada reta:

d. Sustituímos as retas em função de  e resolvemos a integral definida:
e resolvemos a integral definida:
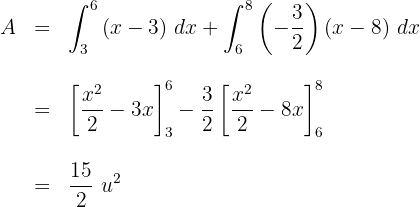
Calcule a área limitada pelos gráfico de 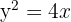 e
e  .
.
a. Primeiro, vamos fazer a representação gráfica das curvas e destacar a área solicitada:
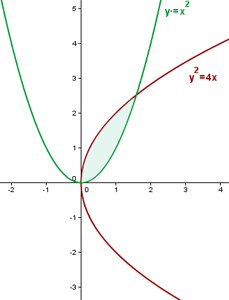
b. Calculamos os limites de integração encontrando os pontos de interseção das curvas:
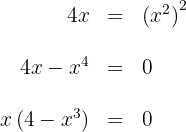
assim,  e
e 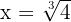 são os limites de integração.
são os limites de integração.
c. A área solicitada é dada pela integral da diferença entre as curvas:
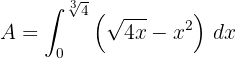
d. Resolvendo a integral definida:

Calcule a área limitada pela curva 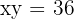 , o eixo
, o eixo  e as retas
e as retas  ,
,  .
.
a. Vamos fazer a representação gráfica das curvas e destacar a área solicitada:
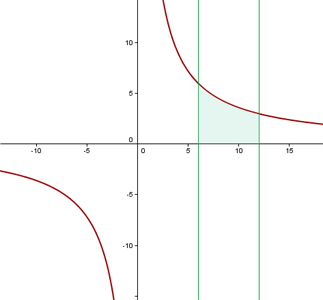
b. A área destacada é definida por:
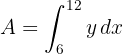
c. Substituimos  em função de
em função de  e resolvemos a integral definida:
e resolvemos a integral definida:
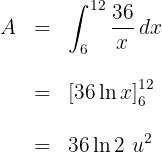
Calcule área limitada pela curva 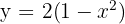 e pela reta
e pela reta 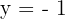 .
.
a. Fazemos o gráfico da curva e da reta e destacamos a área solicitada.
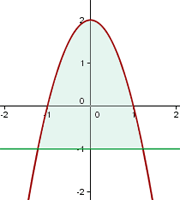
b. Calculamos os limites de integração, para isso buscamos os pontos de interseção das curvas:
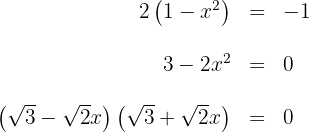
assim,  são os limites de integração.
são os limites de integração.
c. A área solicitada é dada pela integral da diferença entre as duas curvas:
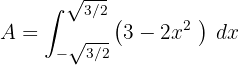
d. Resolvemos a integral definida, observando que a área é simétrica em relação ao eixo 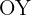

Calcule a área delimitada pela parábola 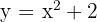 e pela reta que passa pelos pontos
e pela reta que passa pelos pontos  e
e 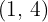 .
.
a. Vamos fazer a representação gráfica da curva e da reta e destacar a área solicitada:
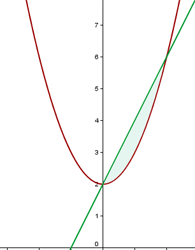
b. Calculamos a inclinação da reta e sua equação:
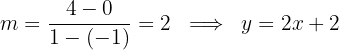
c. Calculamos os limites de integração, para isso, vamos buscar os pontos de interseção das curvas.
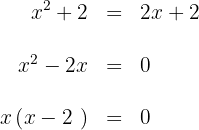
então,  e
e  são os limites de integração.
são os limites de integração.
d. A área desejada é obtida pela integral da diferença dessas curvas:

e. Resolvemos a integral definida:

Determine a área limitada pelas retas 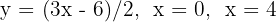 e o eixo de abscissas.
e o eixo de abscissas.
a. Vamos representar as retas e destacar a área solicitada em um gráfico:
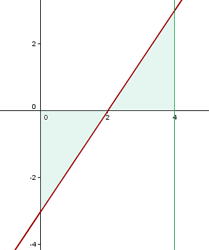
b. A área solicitada é determinada pela integral da região abaixo do eixo  e da região acima desse eixo. Como a área abaixo do eixo é negativa, consideramos seu valor absoluto:
e da região acima desse eixo. Como a área abaixo do eixo é negativa, consideramos seu valor absoluto:
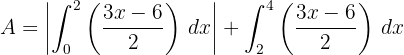
c. Resolvendo a integral definida:
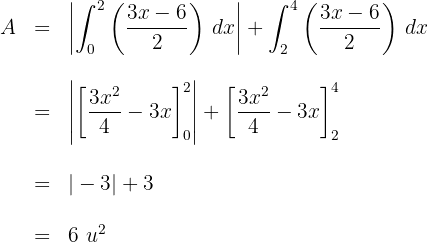
Calcule a área limitada pela curva 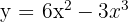 e o eixo de abscissas.
e o eixo de abscissas.
a. Faça uma representação gráfica da curva dada e destaque a área solicitada:
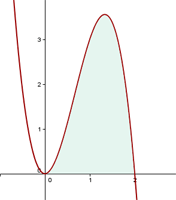
b. Calculamos os limites de integração e para isso, buscamos os pontos de interseção da curva com o eixo das abcissas

então,  e
e  são os limites de integração.
são os limites de integração.
c. A área solicitada é determinada pela integral:

d. Resolvemos a integral definida:
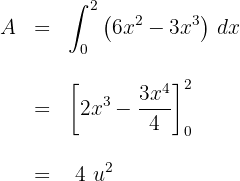
Determine a área da região do plano limitada pelas curvas 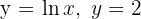 e os eixos coordenados.
e os eixos coordenados.
a. Faça uma representação gráfica das curvas e destaque a área solicitada:
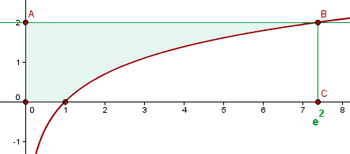
b. A área solicitada é determinada pela integral:

Observamos pela representação gráfica que, ao integrar em relação à variável  , o cálculo se simplifica. Para isso, expressamos a curva em função de
, o cálculo se simplifica. Para isso, expressamos a curva em função de  , ou seja,
, ou seja,
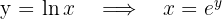
E a área solicitada pode ser expressa como:
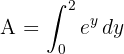
c. Resolvemos a integral definida:
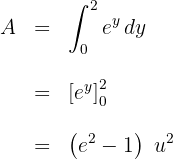
Calcule a área da região do plano limitada pelo círculo 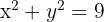 .
.
a. Essa é a representação gráfica da curva dada. Observe que a área solicitada é igual a quatro vezes à área do primeiro quadrante.
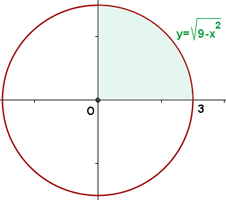
b. Vamos expressar a parte do círculo que está no primeiro quadrante em função de 
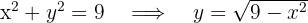
c. A área solicitada é determinada por:
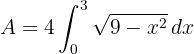
d. Resolvemos a integral definida, para isso, utilizamos a substituição trigonométrica 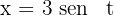 em que a diferencial é
em que a diferencial é 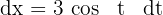 com os seguintes limites de integração:
com os seguintes limites de integração:
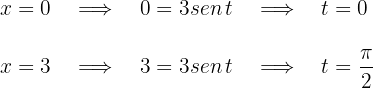
Substituímos os valores de 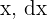 em termos de
em termos de 
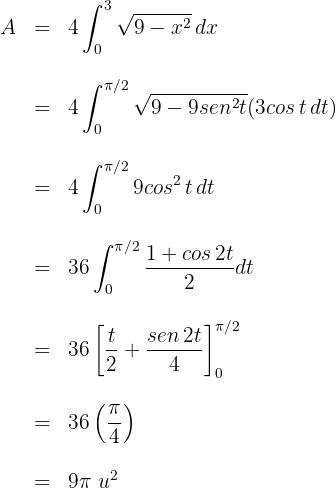
Encontre a área de uma elipse de semieixos  e
e  .
.
a. Representamos graficamente a elipse centrada na origem e com os semieixos dados
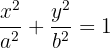
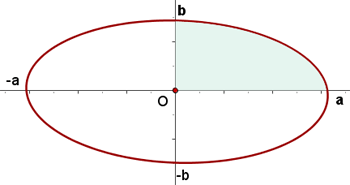
Observamos que a área solicitada é igual a quatro vezes a área do primeiro quadrante.
b. Expressamos a parte da elipse que está no primeiro quadrante em função de 

c. A área solicitada é dada por:

d. Para resolver a integral definida, usamos a substituição trigonométrica:  cuja diferencial é
cuja diferencial é  com os seguintes limites de integração:
com os seguintes limites de integração:

Substituimos os valores de 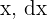 em termos de
em termos de 
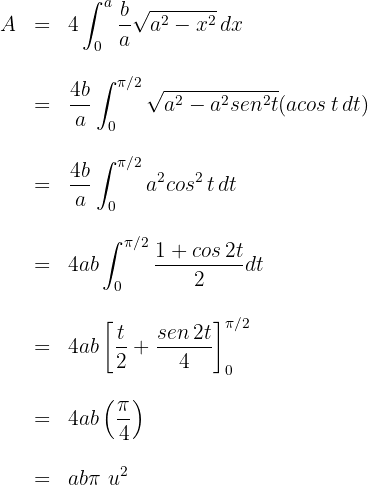
Calcule a área da região do plano limitada pelas raízes da curva 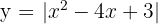 e o eixo
e o eixo  .
.
a. Representação analítica e gráfica da curva e localizamos a área em destaque:
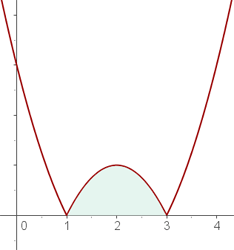
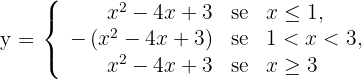
b. Calcule as raízes da curva
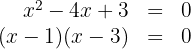
então  e
e  são as raízes da curva.
são as raízes da curva.
c. A área solicitada é determinada por:
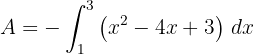
d. Resolvemos a integral definida:
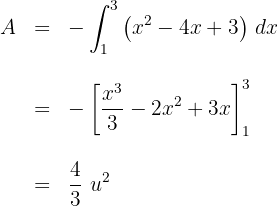
Encontre a área da figura limitada por 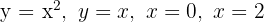 .
.
a. Represenção gráfica da curva e destaque da área solicitada
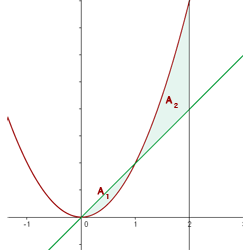
b. Calculamos a interseção entre a reta e a parábola
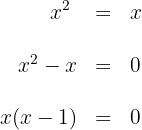
portanto  e
e  são as coordenadas das abscissas onde as duas curvas se interceptam.
são as coordenadas das abscissas onde as duas curvas se interceptam.
c. A área solicitada é determinada em duas partes. Na primera, a reta está em cima da parábola e, na segunda, a parábola está por cima da reta.

Dessa forma, a área solicitada é dada por:
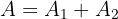
d. Resolvendo as integrais definidas:

Calcule a área da região plana limitada pela parábola 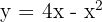 e pelas retas tangentes à curva nos pontos de interseção com o eixo
e pelas retas tangentes à curva nos pontos de interseção com o eixo  .
.
a. Encontramos a interseção com o eixo 
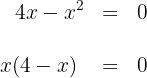
portanto  e
e  são as raizes, e os pontos de interseção são:
são as raizes, e os pontos de interseção são: 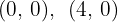 .
.
b. Encontramos a equação da reta tangente em 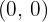

Encontramos a equação da reta tangente em 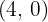

A interseção e as duas retas se encontram em 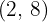
c. Representação gráfica da curva com as tangentes indicadas e a área solicitada destacada.
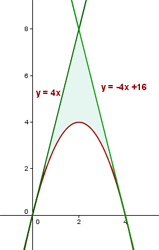
d. A área solicitada é determinada em duas partes. A primeira reta (com inclinação para cima) fica por cima da parábola, e a segunda reta (com inclinação para baixo) também fica por cima da parábola.
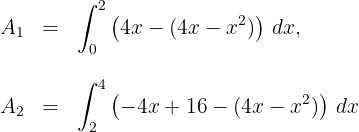
Dessa forma, a área solicitada é determinada por:
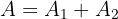
e. Resolvemos as integrais:
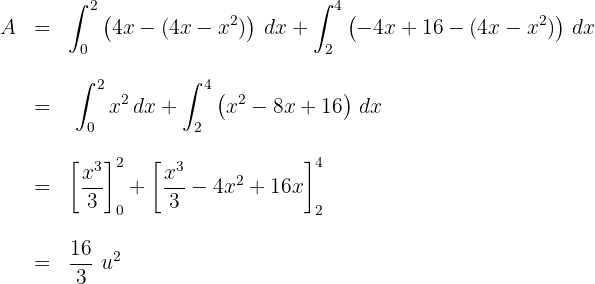
Resumir com IA:


