
Encontre a equação de elipse
Determine a equação do lugar geométrico dos pontos 
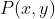
 e
e  seja igual a
seja igual a  .
.
Estamos buscando que soma entre as distâncias  e
e  seja sempre igual a
seja sempre igual a  , ou seja,
, ou seja,

Portanto, temos que:

Uma vez que isolamos a raiz, vamos obter:

Logo, elevando ao quadrado, vamos ter:

Podemos observar que o termo  está presente nos dois lados da equação. Assim, podemos cancelá-lo, e ficamos com:
está presente nos dois lados da equação. Assim, podemos cancelá-lo, e ficamos com:

Se expandirmos os dois binômios ao quadrado, teremos:

Em seguida, reagrupando os termos semelhantes  , e dividindo a equação por
, e dividindo a equação por  —, obtemos:
—, obtemos:

Já eliminamos uma das raízes. Para eliminar a outra, repetimos o procedimento: elevamos a expressão ao quadrado, expandimos os binômios ao quadrado e reagrupamos os termos:

ou seja,

Encontre a equação da elipse de foco  , de vértice
, de vértice  e centro
e centro  .
.
Sabemos que o semieixo maior é a distância entre o centro  e o vértice
e o vértice  , ou seja,
, ou seja,

Da mesma forma, a semidistância focal é a distância entre o centro  e o foco
e o foco  da elipse que corresponde à metade da distância entre os dois focos —, ou seja,
da elipse que corresponde à metade da distância entre os dois focos —, ou seja,

Por fim, o semieixo menor é calculado por meio da fórmula:

Assim, a equação reduzida da elipse é dada por:

Determine a equação da elipse, sabendo que:


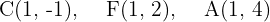
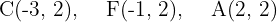

Descreveremos detalhadamente o primeiro item. Os demais serão apresentados de forma mais resumida.
Sabemos que o semieixo maior é a distância entre o centro  e o vértice
e o vértice  , ou seja,
, ou seja,

Da mesma forma, a semidistância focal é a distância entre o centro  e o foco
e o foco  — ou seja, a metade da distância entre os dois focos:
— ou seja, a metade da distância entre os dois focos:
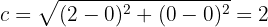
Por fim, o semieixo menor é calculado por:
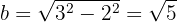
Assim, a equação reduzida da elipse é dada por:

Considerando as próximas equações:

Obtemos que:

Portanto, o semieixo menor é dado por:
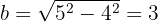
Assim, a equação reduzida da elipse é:

Observe que, neste caso, dividimos  por
por  em vez de
em vez de 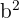 . Isso ocorre porque o eixo maior é vertical (note que os pontos
. Isso ocorre porque o eixo maior é vertical (note que os pontos  ,
,  e
e  têm o mesmo valor na coordenada
têm o mesmo valor na coordenada  ).
).
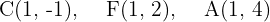
Observe que as coordenadas  dos três pontos é a mesma. Portanto, o eixo maior é vertical. Assim, temos:
dos três pontos é a mesma. Portanto, o eixo maior é vertical. Assim, temos:

Portanto, el semieixo menor está dado por:
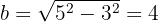
Dessa forma, a equação reduzida da elipse é:

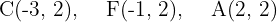
Podemos notar agora que são as coordenadas  as que estão fixas em cada ponto. Deste modo, o eixo maior da elipse será horizontal. Assim, obtemos que:
as que estão fixas em cada ponto. Deste modo, o eixo maior da elipse será horizontal. Assim, obtemos que:

Além disso:

Portanto, a equação será:

Encontre a equação equaçao reduzida de uma elipse sabendo que o eixo maior é o horizontal, um dos focos está a  de distância de um vértice e
de distância de um vértice e  de outro, y cujo o centro está na origem.
de outro, y cujo o centro está na origem.
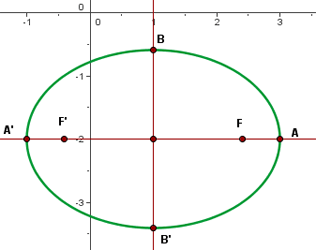
Observa la gráfica de abajo:
Observe o gráfico abaixo:
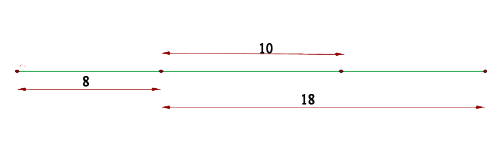
Sabemos que a distância focal deve ser 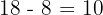 . Deste modo, la semidistância focal é:
. Deste modo, la semidistância focal é:
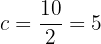
Assim, a distância do centro de qualquer foco. Deste modo, a distância entre a centro e o vértice será:
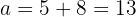
Com esses dados, vamos obter:
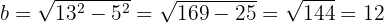
E portanto, a equação da elipse é:

Encontre a equação reduzida de uma elipse sabendo que ela passa pelo ponto  , tem centro na origem, eixo maior horizontal e excentricidade igual a
, tem centro na origem, eixo maior horizontal e excentricidade igual a 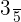 .
.
Como a elipse tem centro na origem, sua equação reduzida será da forma:

Além disso, sabemos que a elipse passa pelo ponto  . Isso significa que esse ponto deve satisfazer a equação da elipse. Substituindo os valores, temos:
. Isso significa que esse ponto deve satisfazer a equação da elipse. Substituindo os valores, temos:
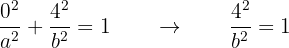
Isolamos 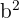 , obtemos:
, obtemos: 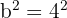 . Logo, uma vez que
. Logo, uma vez que 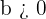 , temos que:
, temos que:

Agora, utilizamos a fórmula da excentricidade, que é dada por:

Se elevamos ao quadrado:
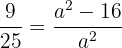
Multiplicamos a equação por  , e em seguida por
, e em seguida por  para obter:
para obter:
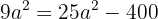
Reagrupando os termos:

Ou seja,  .
.
Portanto, a equação reduzida da elipse é:

Determine a equação reduzida da elipse com centro na origem, que passa pelo ponto  e cujo o eixo menor mede
e cujo o eixo menor mede  e é vertical.
e é vertical.
Como a elipse tem centro na origem, sua equação reduzida será da forma:

Além disso, como o eixo meno tem a medida de  , então o semieixo menor é:
, então o semieixo menor é:
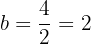
Logo, como a elipse passa pelo ponto  , então deve satisfazer a equação:
, então deve satisfazer a equação:
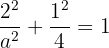
Isolando  obtemos:
obtemos:
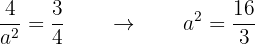
De forma que:

Assim, a equação reduzida da equação da elipse é:
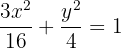
A distância focal de uma elipse com centro na origem és  e os focos se encontram sobre o eixo x. Um ponto da elipse está distante de seus focos
e os focos se encontram sobre o eixo x. Um ponto da elipse está distante de seus focos  e
e  , respectivamente. Calcule a equação reduzida da elipse.
, respectivamente. Calcule a equação reduzida da elipse.
Conhecemos a distância focal, que é de  . Portanto, a semidistância focal é:
. Portanto, a semidistância focal é:
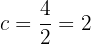
Mesmo assim, a soma das distâncias de qualquer ponto entre os focos sempre sera constante. Esta distância coincide com o eixo maior, de modo que:

Finalmente, o semieixo meienor::
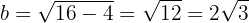
Assim, a equação reduzida da elipse é:
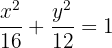
Determine a equação da elipse com centro na origem, focos sobre o eixo x, e que passa pelos pontos 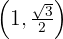 e
e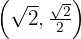 .
.
Como a elipse passa por ambos os pontos, então deverá satisfazer o seguinte sistema de equações:
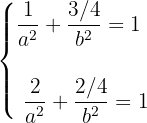
Trata-se de um sistema não linear com dois incógnitas (no link você aprende como resolvê-lo). Neste caso, utilizamos uma mudança de variável:

A solução do sistema é:

Para fazer a verificação, substitua os valores de  e
e  no sistema não linear original.
no sistema não linear original.
Portanto, a equação da elipse é:

Determine a equação da elipse com centro na origem, cuja distância focal é  , focos sobre o eixo x, e a área do retângulo construído sobre os eixos é de
, focos sobre o eixo x, e a área do retângulo construído sobre os eixos é de  .
.
A distância focal é  . Portanto, temos que:
. Portanto, temos que:

Além disso, os semieixos maior e menor satisfazem a relação clássica entre  ,
,  e
e  dada por:
dada por:
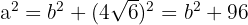
Por outro lado, temos um retângulo cujos lados medem  y
y  . A área desse retângulo é:
. A área desse retângulo é:

Portanto, precisamos resolver o seguinte sistema de equações não lineares:
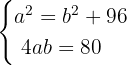
Esse sistema não linear pode ser resolvido isolando  na segunda equação e substituindo seu valor na primeira. Dessa forma, obtemos uma equação do quarto grau com potências pares. A solução do sistema é:
na segunda equação e substituindo seu valor na primeira. Dessa forma, obtemos uma equação do quarto grau com potências pares. A solução do sistema é:
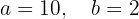
Portanto, a equação da elipse é:

Encontre elementos a partir da equação
Determine os elementos característicos e a equação reduzida da elipse com os focos:  e
e 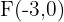 , e com eixo maior que mede
, e com eixo maior que mede  .
.
Determine os elementos característicos e a equação reduzida da elipse com os focos:  e
e 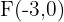 , e com eixo maior que mede
, e com eixo maior que mede  .
.
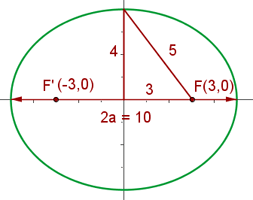
Semieixo maior
Temos que 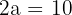 , portanto, o semieixo maior é
, portanto, o semieixo maior é  .
.
Semidistância focal:
Aqui temos que a distância entre os dois focos é de 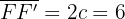 . Dessa forma, a semidistância focal é
. Dessa forma, a semidistância focal é  .
.
Semieixo menor
Temos que  onde
onde  é o semieixo menor. Deste modo,
é o semieixo menor. Deste modo,
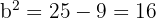
Assim, o semieixo menor mede  .
.
Equação reduzida
Uma vez que temos os valores de  e
e  , bem como o do centro —que é dado pelo ponto médio dos focos, ou seja,
, bem como o do centro —que é dado pelo ponto médio dos focos, ou seja,  —, então a equação reduzida está dada por:
—, então a equação reduzida está dada por:

Excentricidade:
Por fim, a excentricidade da elipse é dada por:
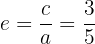
Dada a equação reduzida da elipse 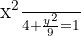 , determine as coordenadas dos vértices, dos covértices, dos focos e a excentricidade
, determine as coordenadas dos vértices, dos covértices, dos focos e a excentricidade
Pela forma da equação, sabemos que a elipse tem centro na origem. Além disso, temos:

os vértices tem as coordenadas

e o eixo maior está sobre o eixo  . Os covértices se encontram em:
. Os covértices se encontram em:

Logo, temos que a semidistância focal é:
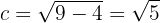
Deste modo, os focos se encontran em:
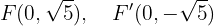
Finalmente, a excentricidade se encontra mediante:
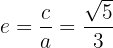
Considerando a elipse da equação  , encontre o centro, semieixos, vértices, covértices e focos.
, encontre o centro, semieixos, vértices, covértices e focos.
A partir da equação, concluímos imediatamente que o centro da elipse está no ponto  . Além disso, os semieixos menor e maior são:
. Além disso, os semieixos menor e maior são:
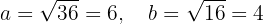
Portanto:
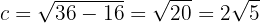
Deste modo, os vértices se encontram em 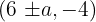 , ou seja,
, ou seja,
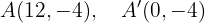
Logo, os focos estão em:

Os covértices se encontram nos pontos:
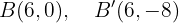
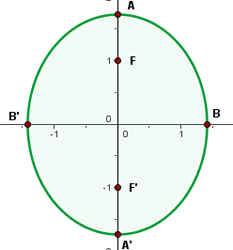
Represente graficamente e determine as coordenadas dos focos, dos vértices, dos covértices e da excentricidade das seguintes elipses:
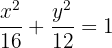
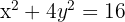

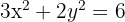
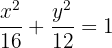
O centro está na origem. O semieixos menor e maior são:

Desta maneira, os vértices estão em:
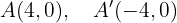
Os covértices se encontram nos pontos:
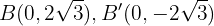
A semidistância focal é:
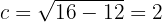
E os focos estão em:
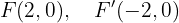
Finalmente, a excentricidade está:

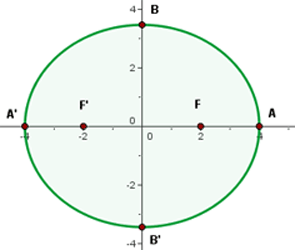
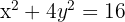
Primeiro, vamos escrever a equação de forma reduzida e então dividir por  :
:

Logo, a partir da equação, conclui-se que o centro está na origem, ou seja, 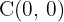 , e que
, e que

E que os vértices se encontram em:
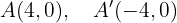
e os covértices estão em:

Além disso, a semidistância focal é:
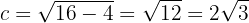
Assim, os focos se encontram em:
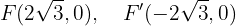
Finalmente, a excentricidade é dada por:

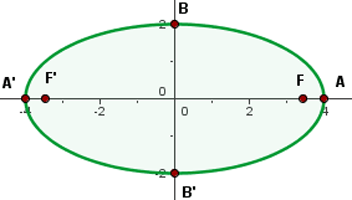

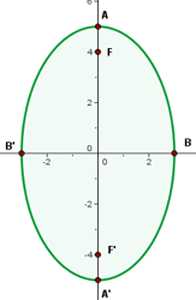
A equação já está em sua forma reduzida.Da equação, pode-se observar que o centro da elipse está no ponto 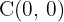 . Além disso, os semieixos menor e maior são dados por:
. Além disso, os semieixos menor e maior são dados por:
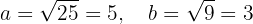
A semidistância focal é dada por:
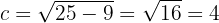
Observe que o eixo maior está sobre o eixo  . Deste modo, os vértices se encontram em:
. Deste modo, os vértices se encontram em:
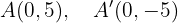
Os covértices estão em:

E os focos estão nos pontos:
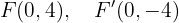
Finalmente, a excentricidade está dada por:

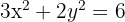
Por último, temos uma equação que ainda não está em sua forma reduzida. Primeiro, dividimos por  para obter:
para obter:
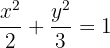
A partir da equação temos que:

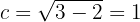
Além disso, observamos que o eixo maior está sobre o eixo  . Deste modo, os vértices estão:
. Deste modo, os vértices estão:
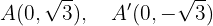
Os covértices estão nos pontos:

E os focos estão localizados em:
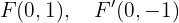
Por último, a excentricidade é:
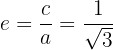
Represente graficamente e determine as coordenadas dos focos, dos vértices e dos covértices das elipses a seguir:

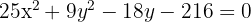



Para determinar os pontos importantes da elipse, precisamos escrever sua equação na forma reduzida. Para isso, utilizamos o método de completar quadrados.
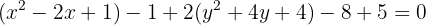
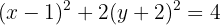
Em seguida, dividimos por  ,
,
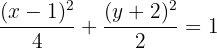
Deste modo, é possível ver que o centro está em  . Além disso, também é possível identificar que:
. Além disso, também é possível identificar que:
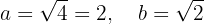
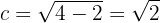
Logo, o eixo maior é horizontal, e os vértices se encontram em:
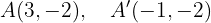
E os covértices em:

E os focos se encontram em:

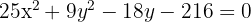
Vamos completar o quadrado novamente:
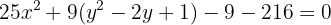

Em seguinda, dividimos por  ,
,
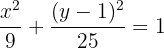
Daqui, é possível ver que o centro está  . Além disso, podemos identificar que:
. Além disso, podemos identificar que:
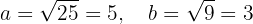
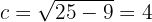
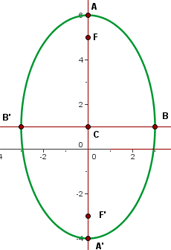
Logo, o eixo maior é vertical, uma vez que vértices se encontram em:
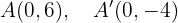
Os covértices se encontram em:
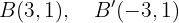
E os focos em:


Completamos o quadrado de novo:
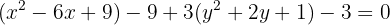
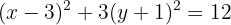
E em seguida, dividimos por  ,
,
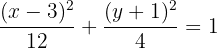
Deste modo, é possível ver que o centro está em  e identificar que:
e identificar que:
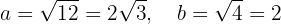

Logo, o eixo maior é horizontal, uma vez que os vértices se encontram em:

Os covértices se encontram em:
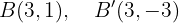
E os focos em:


Vamos completar o quadrado de novo:


Em seguida, dividimos por  ,
,
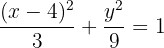
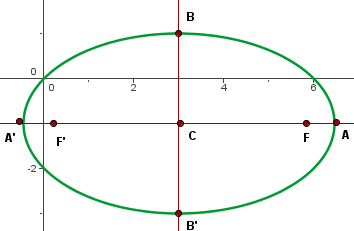
É possível ver que o centro está em  . Além disso, é possível identificar que:
. Além disso, é possível identificar que:
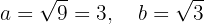
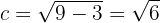
Logo, o eixo maior é vertical, já que os vértices se encontram em:

Os covértices se encontram em:

E os focos se encontram em
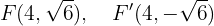
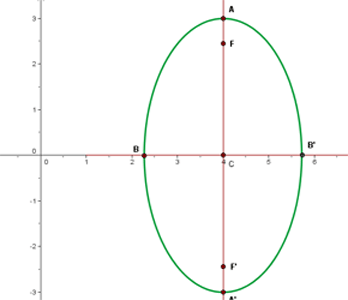
Encontre as coordenadas do ponto médio da corda formada pela interseção da reta 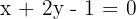 com a elipse de equação
com a elipse de equação 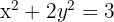 .
.
Primeiro, observe o gráfico da reta e da elipse:
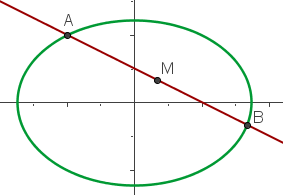
A partir de la figura podemos deduzir que devemos encontrar as coordenadas dos pontos  e
e  . Logo,
. Logo,  está será o ponto médio dos dois.
está será o ponto médio dos dois.
Encontrar as coordenadas de  e
e  é o equivalente a resolver o sistema não linear de equações dado por:
é o equivalente a resolver o sistema não linear de equações dado por:
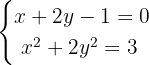
Este sistema também é resolvido por substituição. As soluções são dadas por:

Portanto, o ponto médio da corda está dado por
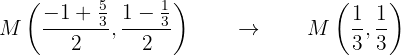
Resumir com IA:












