Temas

Método de conversão de decimais para frações
Para converter decimais em frações, é importante ter em mente três ideias fundamentais:
- Quando o decimal não for periódico, dividimos por 1, 10, 100, 1000... conforme a quantidade de casas decimais.
- Quando os decimais forem totalmente periódicos, dividimos por
9, 99, 999… de acordo com o número de algarismos que se repetem. - Quando o número tiver uma parte decimal periódica e outra não periódica, utilizamos denominadores do tipo 90, 900, 9000…
Vamos usar estes três números como exemplo: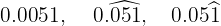
No primeiro caso, temos um número com quatro casas decimais e nenhuma é periódica.
Para convertê-lo para fração, basta colocar 51 no numerador e, no denominador, 1 seguido de quatro zeros, já que são quatro casas decimais. Assim, obtemos:
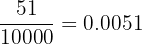
No segundo caso, o número possui três casas decimais, e as três são periódicas. Portanto, usamos como numerador o número 51 e, como denominador, três noves, pois são três algarismos que se repetem. Assim, fica:

No terceiro caso, o número tem três casas decimais, mas apenas uma delas é periódica. Para montar a fração, o numerador será 51 − 5, pois o 5 é a parte não periódica. O denominador será 900, pois usamos um 9 (para o algarismo periódico) e dois zeros (para as duas casas não periódicas).
Lembrando: usamos 9 para cada algarismo periódico e 0 para cada algarismo não periódico. Assim, temos:

Depois, se possível, simplificamos as frações.
Converta os seguintes decimais em frações
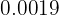
Trata-se de um número com 4 casas decimais e nenhuma delas é periódica.
Para convertê-lo em fração, basta colocar o 19 no numerador e, no denominador, escrever o número 1 seguido de quatro zeros, já que são 4 casas decimais.
Desse modo, temos:
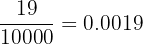
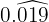
No numerador, escrevemos o número sem a vírgula e, no denominador, colocamos três noves, porque há 3 algarismos periódicos.
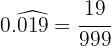
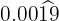
No numerador, escrevemos o número sem a vírgula e, no denominador, colocamos dois algarismos 9 e dois zeros, porque há um algarismo no período e duas casas decimais.
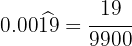
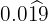
No numerador, escrevemos o número sem a vírgula e, no denominador, colocamos dois algarismos 9 e um zero, porque temos dois algarismos no período e uma casa decimal.
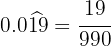
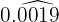
No numerador, escrevemos o número sem a vírgula e, no denominador, colocamos quatro algarismos 9.
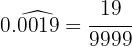
Efetue as seguintes operações com potências
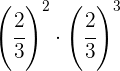
Para multiplicar potências de mesma base, somamos os expoentes.
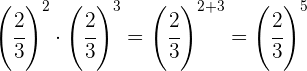
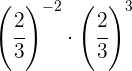
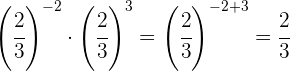
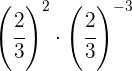
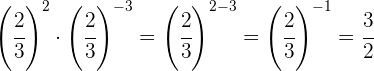
Para eliminar o sinal negativo do expoente, precisamos escrever a fração inversa.
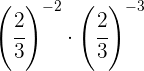
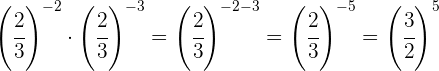
Para eliminar o sinal negativo do expoente, precisamos escrever a fração inversa.
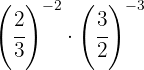
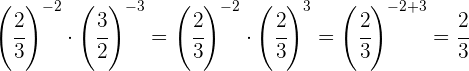
Como as potências não têm a mesma base, tomamos a fração inversa da segunda potência porque o expoente dela era negativo.
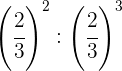
Para dividir potências de mesma base, subtraímos os expoentes.
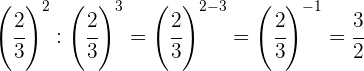
Tomamos a fração inversa, e por isso mudamos o sinal do expoente.
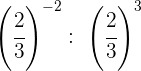
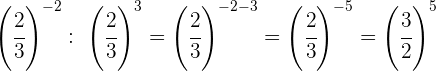
Mudamos o sinal do expoente tomando a fração inversa.
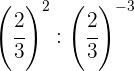
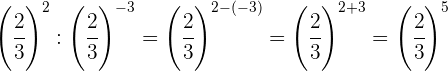
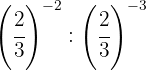
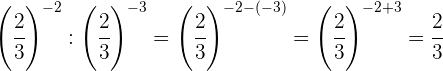
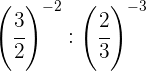
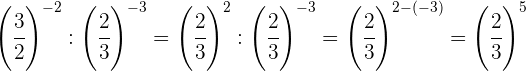
Tomamos a fração inversa da primeira potência para mudar o sinal do expoente
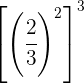
Para multiplicar potências de mesma base, multiplicam-se os exponentes
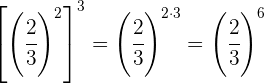
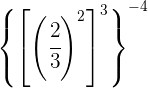
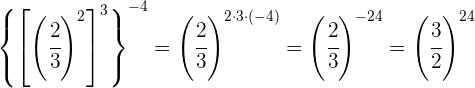
Tomamos a fração inversa da primeira potência para mudar o sinal do expoente
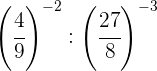
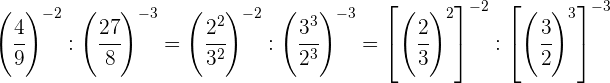
Decompomos os números em fatores; dentro de cada parêntese, dividimos potências que têm o mesmo expoente, portanto dividimos as bases e mantemos o mesmo expoente}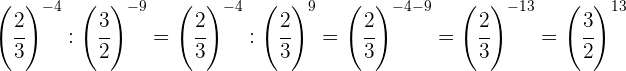
Tomamos a fração inversa da primeira potência para mudar o sinal do expoente e fazemos o mesmo com o resultado.
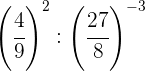
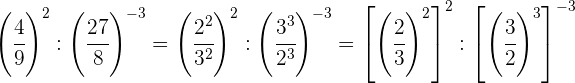
Descomponemos los números en factores, dentro de cada paréntesis
dividimos potencias con el mismo exponente, por tanto dividimos las
bases y dejamos el mismo exponente
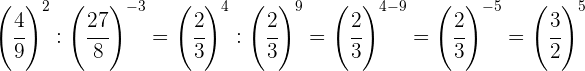
Tomamos la fracción inversa de la primera potencia para cambiar el signo del exponente y hacemos lo mismo con el resultado
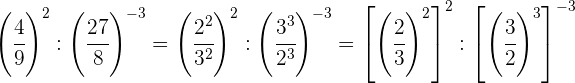
Decompomos os números em fatores e, dentro de cada parêntese, dividimos potências com o mesmo expoente; portanto, dividimos as bases e mantemos o mesmo expoente.
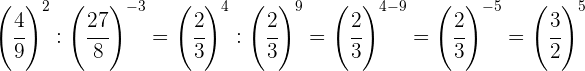
Tomamos a fração inversa da primeira potência para mudar o sinal do expoente e fazemos o mesmo com o resultado.
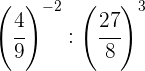
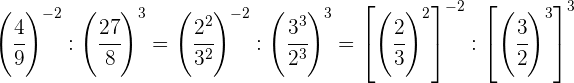
Decompomos os números em fatores e, dentro de cada parêntese, dividimos potências com o mesmo expoente; portanto, dividimos as bases e mantemos o mesmo expoente.
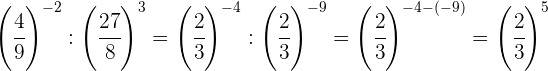
Tomamos a fração inversa da primeira potência para mudar o sinal do expoente e fazemos o mesmo com o resultado.
Efetue as operações a seguir
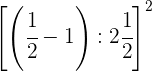
Convertemos o número misto 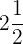 em fração.
em fração.
Mantemos o mesmo denominador (2) e o numerador é a soma da multiplicação da parte inteira (2) pelo denominador (2) mais o numerador do número misto (1).
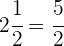
Reduzimos as frações ao mesmo denominador.
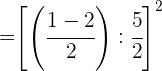
Realizamos as operações nos numeradores.
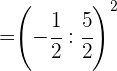
Dividimos.
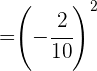
Simplificamos e efetuamos a potência.
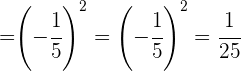
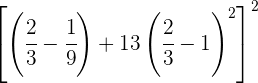
Reduzimos as frações ao mesmo denominador.
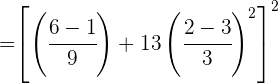
Realizamos as operações nos numeradores.
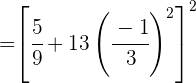
Efetuamos a potência.
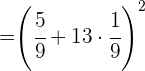
Multiplicamos.
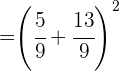
Fazemos a soma e efetuamos a potência.
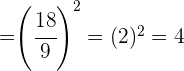
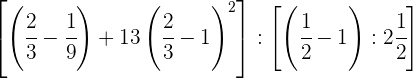
Convertemos o número misto 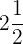 em fração.
em fração.
Mantemos o mesmo denominador (2) e o numerador é a soma da multiplicação da parte inteira (2) pelo denominador (2) mais o numerador do número misto (1).
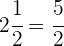
Reduzimos as frações de cada parêntese ao mesmo denominador.
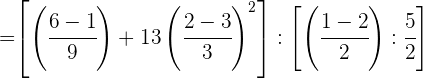
Realizamos as operações nos numeradores.
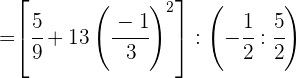
Efetuamos a potência.
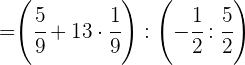
Multiplicamos no primeiro parêntese e dividimos no segundo.
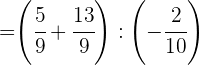
Fazemos a soma no primeiro parêntese e simplificamos no segundo.
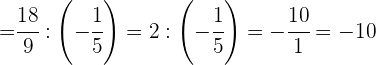
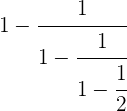
Em primeiro lugar, efetuamos a última parte do denominador.
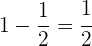
Fazemos o inverso.
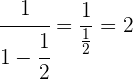
Realizamos a subtração.
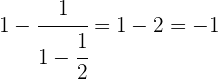
Fazemos o inverso.
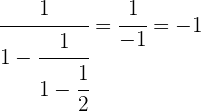
Realizamos a subtração.
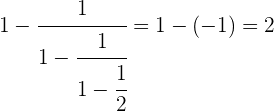
Realizando os passos de forma consecutiva, obtemos:
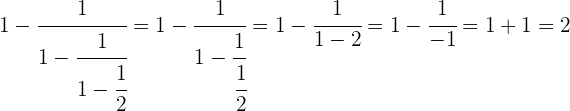
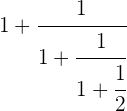
Em primeiro lugar, efetuamos a última parte do denominador.
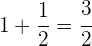
Fazemos o inverso.
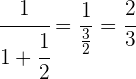
Realizamos a soma.
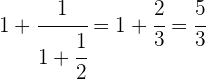
Fazemos o inverso.
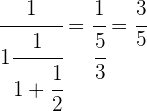
Realizamos a soma.
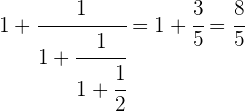
Realizando os passos de forma consecutiva, obtemos:
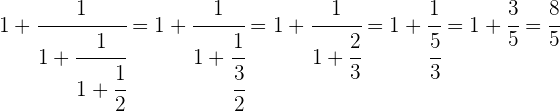
Calcule que fração da unidade cada caso representa
A metade da metade.
A metade da metade.
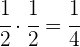
A metade da terceira parte
A metade da terceira parte
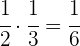
A terceira parte da metade
A terceira parte da metade:
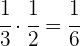
A metade da quarta parte
A metade da quarta parte
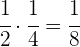
A metade da quarta parte de um terço
A metade da quarta parte de um terço
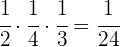
Aplicações
Elena vai às compras com R$ 180. Ela gasta 3/5 desse valor. Quanto sobra para ela?
Para encontrar 3/5 de 180, precisamos multiplicar por 3 e dividir o resultado por 5.
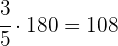 R$
R$
Ela ficará com o valor original (180) menos os 3/5 gastos (108).
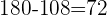 R$
R$
Dois automóveis, A e B, percorrem o mesmo trajeto de 572 km.
O automóvel A já completou 5/11 do percurso quando o B já percorreu 6/13 do mesmo trajeto.
Qual dos dois está na frente? Quantos quilômetros cada um percorreu?
Vamos comparar os percursos de A e B.
Para isso, colocamos as frações em denominador comum; aquela que tiver o maior numerador corresponde ao maior percurso.
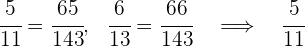
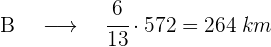
Hace unos años Pedro tenía 24 años, que representan los 2/3 de su edad actual. ¿Qué edad tiene Pedro?
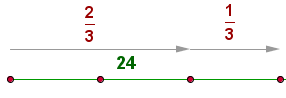
Os 24 anos equivalem a duas partes da idade; então calculamos quanto vale uma parte (24 ÷ 2) e, em seguida, multiplicamos o resultado pelo número total de partes (3).
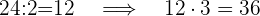 años
años
Nas eleições municipais realizadas em uma cidade, 3/11 dos votos foram para o partido A, 3/10 para o partido B, 5/14 para C e o restante para o partido D.
O total de votos foi de 15 400. Calcule:
O número de votos obtidos por cada partido.
O número de abstenções, sabendo que o número de votantes corresponde a 5/8 do colégio eleitoral.
Calculamos os votos de cada um dos partidos:
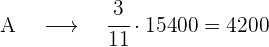 votos
votos
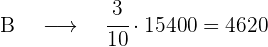 votos
votos
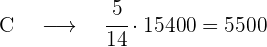 votos
votos
O partido D terá o total de votos menos a soma dos votos recebidos pelos outros partidos.
O total de votantes corresponde a 8/8, ou seja, representa 1 (o total).
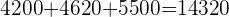
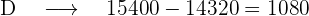
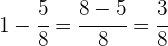

A reta está dividida em 8 partes iguais.
Para saber quanto representa cada parte, observamos que as 5 primeiras partes (a dos votos) somam 15 400; portanto, uma parte será 15400 dividido por 5, o que resulta em 3 080. E as outras três partes (as das abstenções) serão obtidas multiplicando 3 por 3 080.
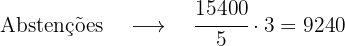
Um pai reparte entre seus filhos R$ 1 800.
Ao mais velho ele dá 4/9 desse valor, ao do meio 1/3 e ao mais novo o restante. Vamos calcular quanto cada um recebeu.
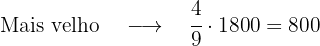
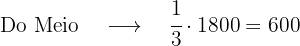
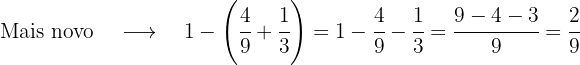
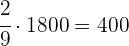
Resumir com IA:












