Temas

Recursos chave para resolver os exercícios propostos
Para resolver os exercícios seguintes, é necessário ter à mão as seguintes ferramentas:
- Círculo unitário
- Identidades trigonométricas básicas
- Identidade fundamental da trigonometria
- Identidades trigonométricas pares e ímpares
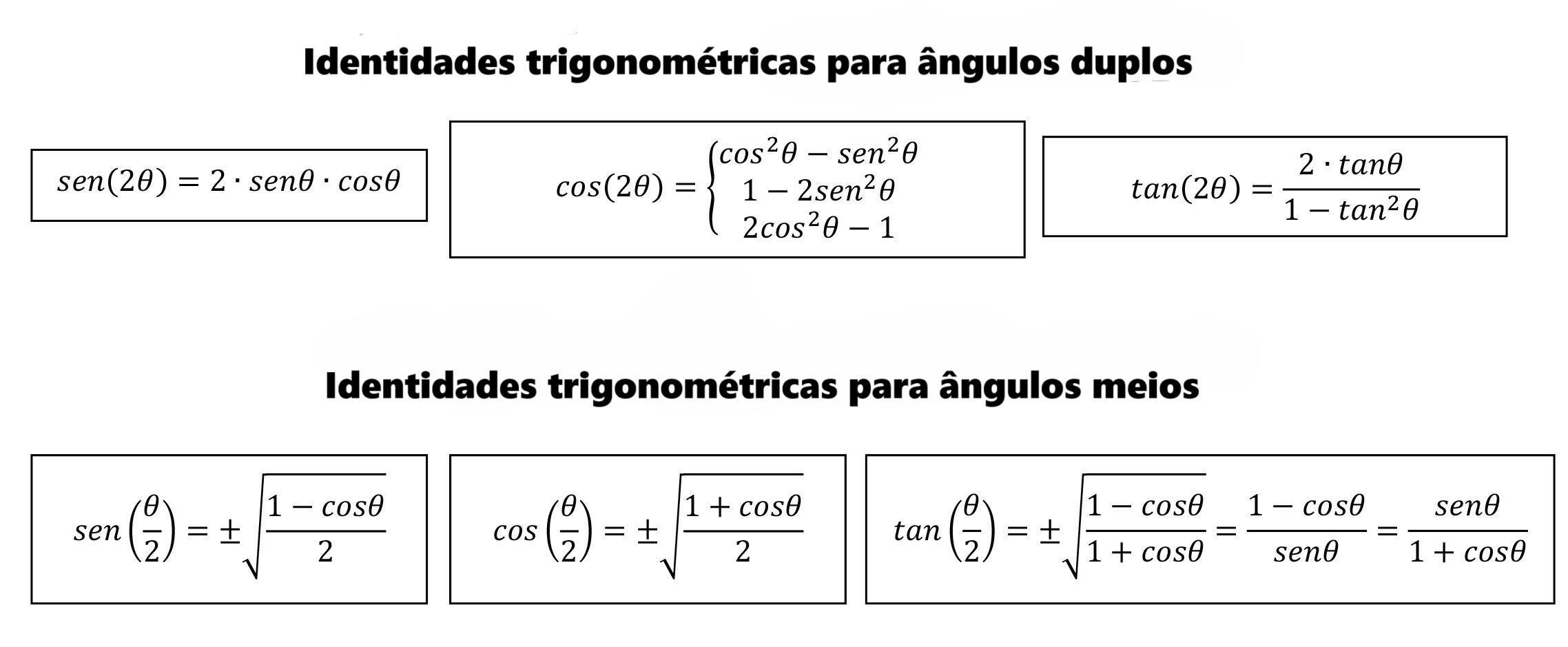
- Identidades trigonométricas para ângulos duplos
- Identidades trigonométricas para ângulos meios
- Soma e subtração de ângulos e relações produto-soma
Círculo unitário
A tabela conhecida como círculo unitário, que contém os valores dos ângulos mais representativos usados na trigonometria, além disso, o nome deste círculo se deve ao fato de ser um círculo com raio 1.
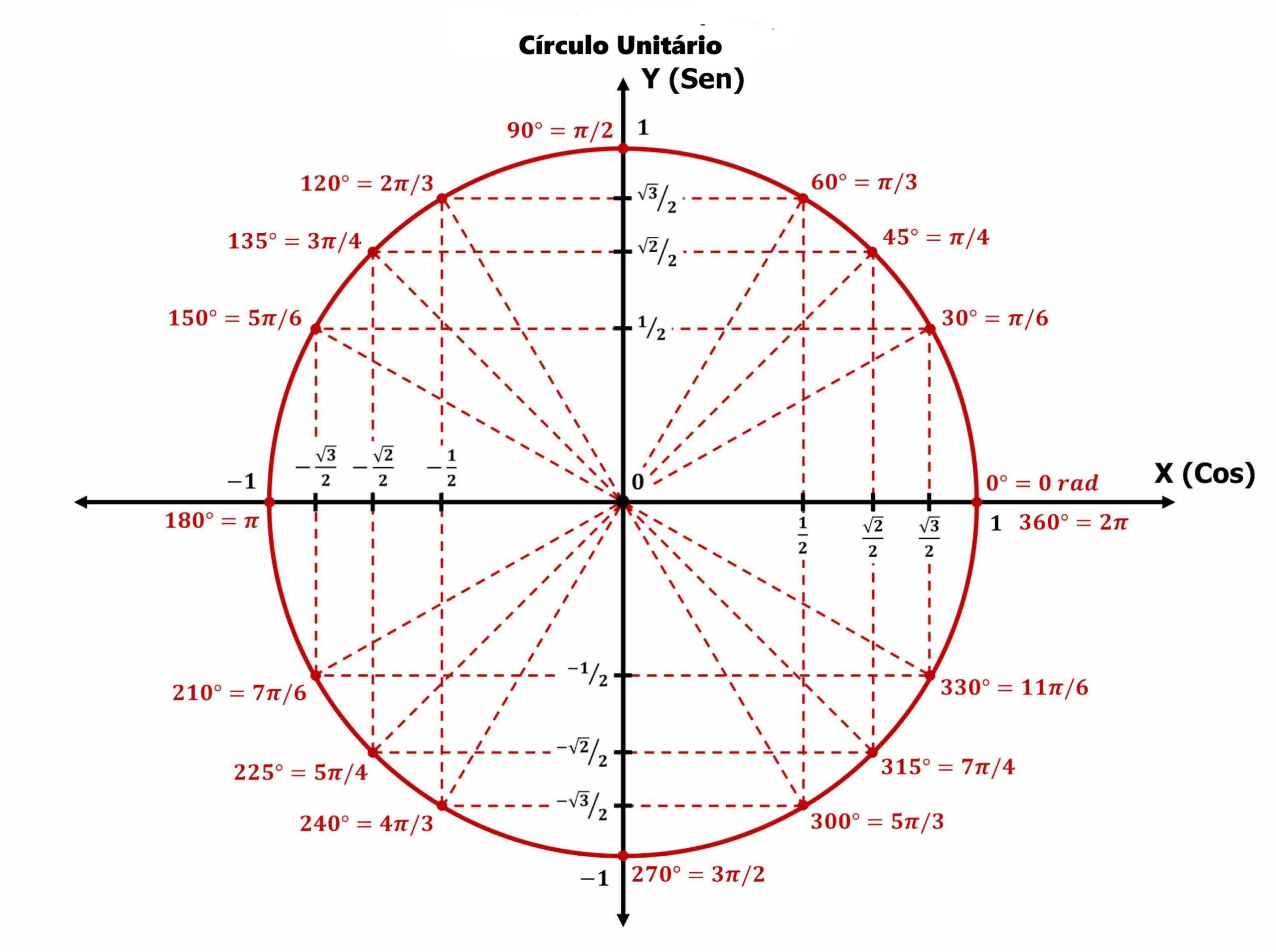
Com esta ferramenta será muito simples localizar o valor dos ângulos. Por exemplo, se quisermos conhecer o valor de 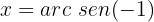 , basta localizarmos no eixo do seno, ou seja, o eixo
, basta localizarmos no eixo do seno, ou seja, o eixo  , e depois encontrar o valor
, e depois encontrar o valor  .
.
Notaremos que a tabela indica que o ângulo é 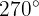 é o valor em graus. Mas também existe o valor em radianos, que é
é o valor em graus. Mas também existe o valor em radianos, que é 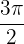
Quando precisamos localizar os valores para a tangente, lembramos que a tangente é uma linha reta que toca a circunferência em um único ponto. No caso desta circunferência, a tangente utilizada é aquela que toca o ponto de  e a altura da tangente dependerá do valor na equação. Por exemplo, na equação
e a altura da tangente dependerá do valor na equação. Por exemplo, na equação  isolamos a variável e obtemos
isolamos a variável e obtemos 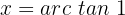 , então, buscamos a tangente com altura igual a
, então, buscamos a tangente com altura igual a  e traçamos a linha até o origem. Observamos o ponto onde a linha se intersecta com a circunferência e procuramos o valor na tabela.
e traçamos a linha até o origem. Observamos o ponto onde a linha se intersecta com a circunferência e procuramos o valor na tabela.
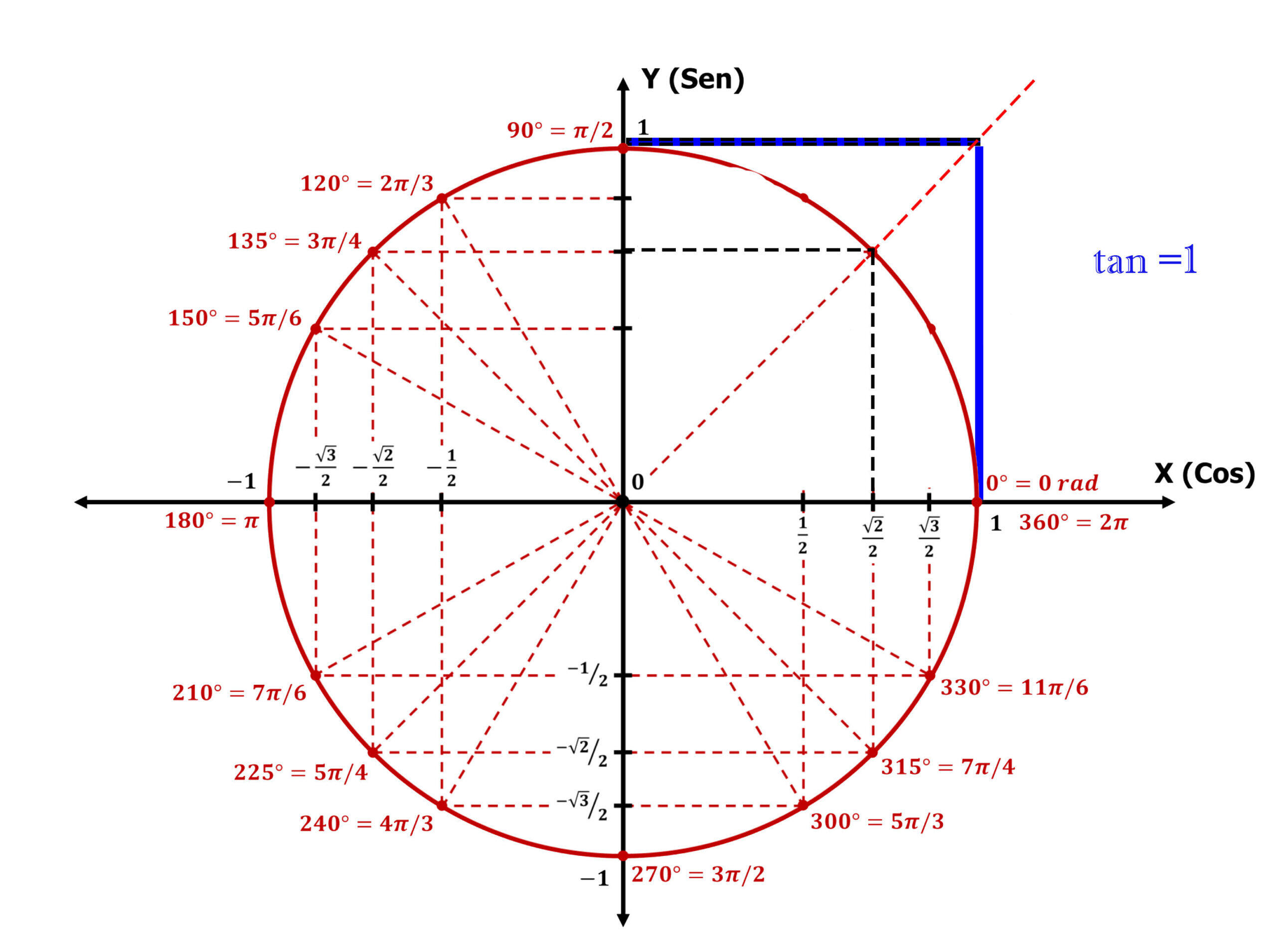
Ou seja, corresponde a 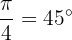
Também poderia dizer que corresponde a 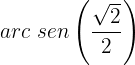 ou
ou 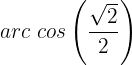
Identidades trigonométricas básicas
As identidades trigonométricas são igualdades definidas que nos ajudam a realizar o trabalho algébrico sem complicação.
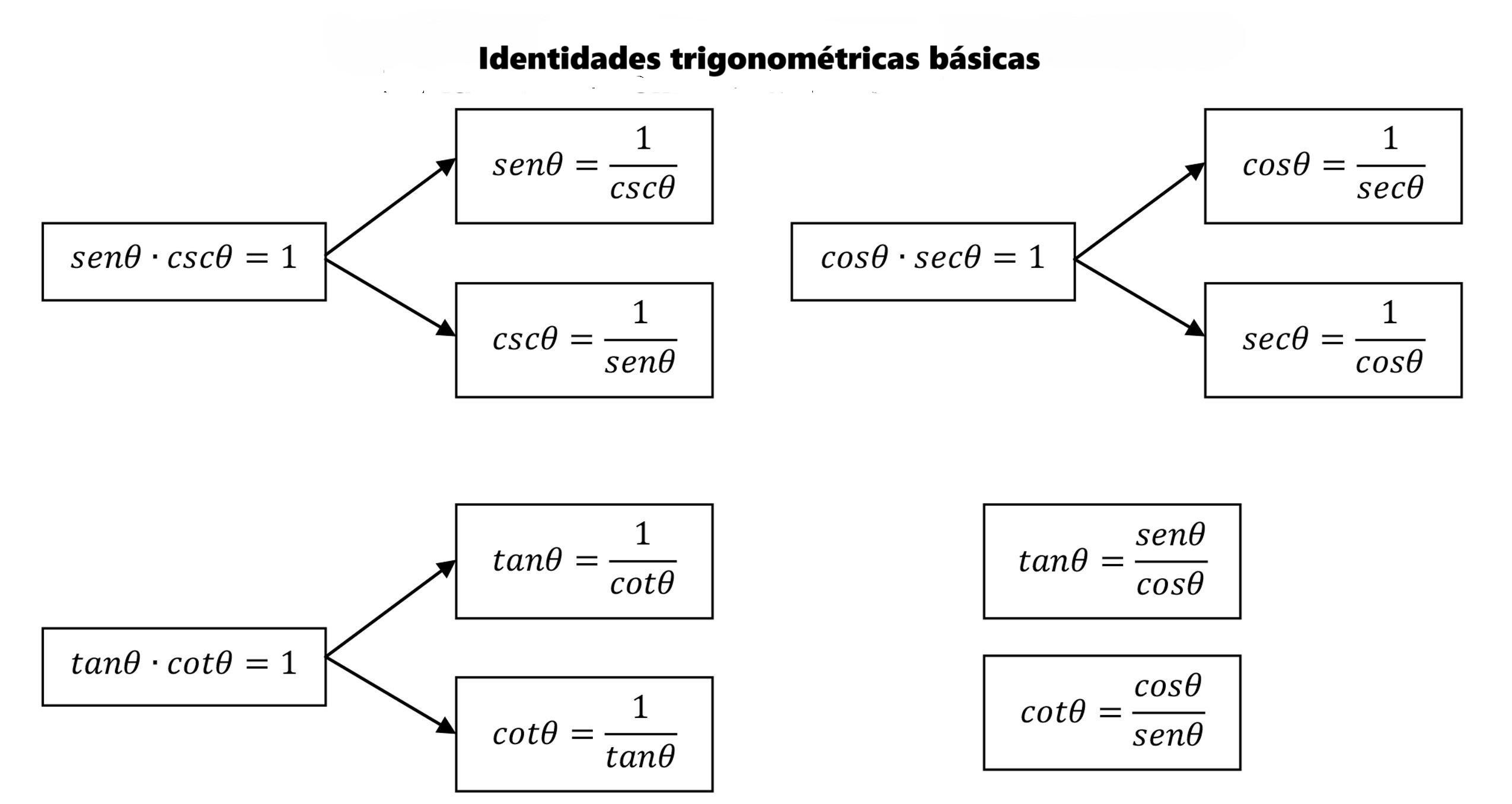
Identidade fundamental da trigonometria
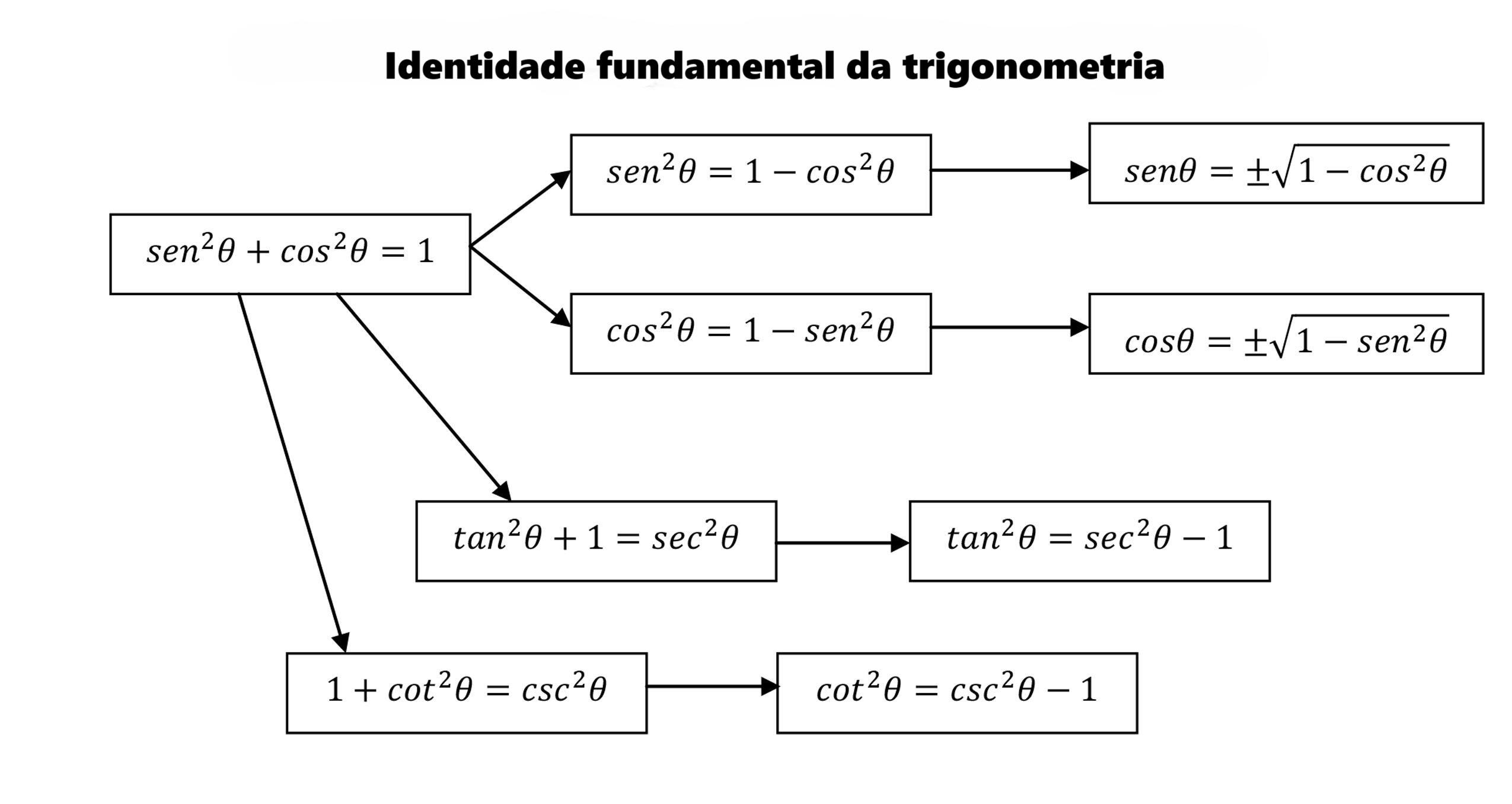
Identidades trigonométricas pares e ímpares
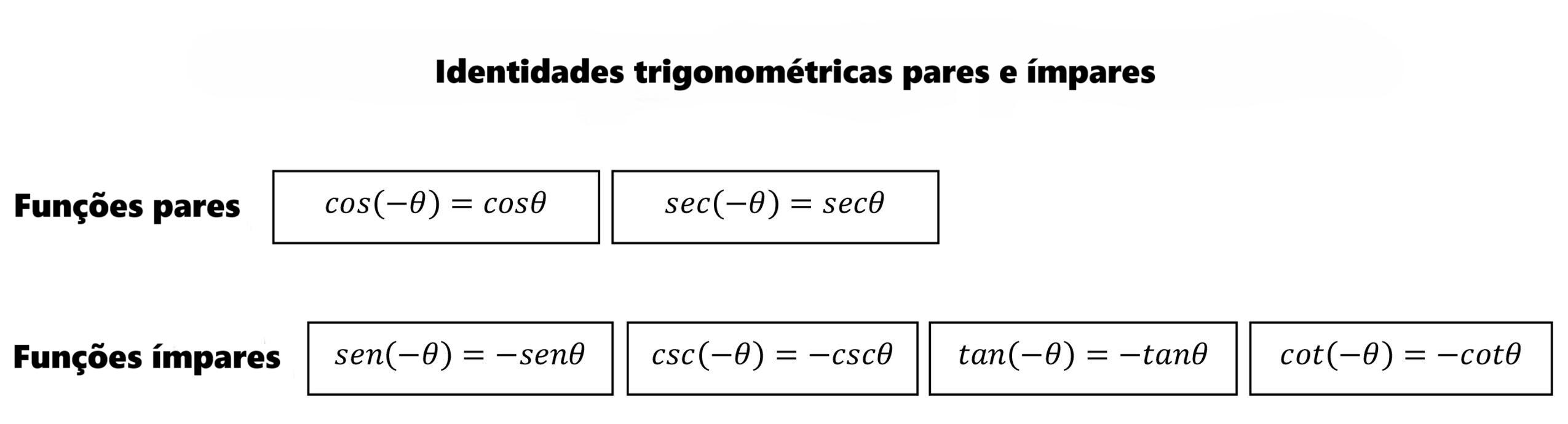
Identidades trigonométricas para ângulos duplos e ângulos médios
Soma e subtração de ângulos e relações produto-soma

Exercícios de equações trigonométricas básicas
Resolva isolando a variável e localizando os valores no círculo unitário.
1 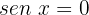
2 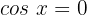
3 
4 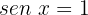
5 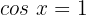
6 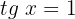
7 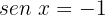
8 
9 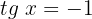
10 
11 
12 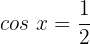
13 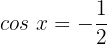
Para resolver as seguintes equações trigonométricas, é necessário recordar a propriedade da função inversa:
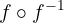 =x
=x
1 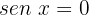
Para resolver essa equação, isolamos a variável x e utilizar a propriedade da função inversa:
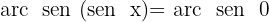
Consultando a tabela, encontramos o valor de 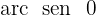
Nos posicionamos no eixo y (o eixo do seno), localizamos o valor 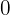 no eixo,e, por fim, observamos os pontos que atravessam a circunferência e passam por
no eixo,e, por fim, observamos os pontos que atravessam a circunferência e passam por 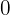 . Esses valores serão o resultado da equação:
. Esses valores serão o resultado da equação:
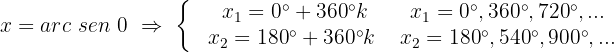

2 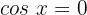
Isolamos o x, utilizamos a propriedade da função inversa:
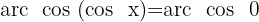
Na tabela, vemos que a tangente de 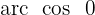
Nos posicionamos no eixo do cosseno, ou seja, no eixo x, agora localizamos o valor 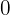 eno eixo, e, por fim, nos deslocamos até os pontos que atravessam a circunferência e passam por
eno eixo, e, por fim, nos deslocamos até os pontos que atravessam a circunferência e passam por 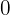 . Esses valores serão o resultado da equação:
. Esses valores serão o resultado da equação:
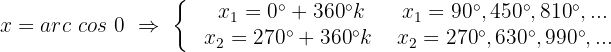
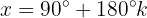
3 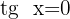
Isolamos a variável x, fazendo uso da propriedade do inverso:
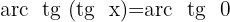
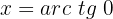
Na tabela, visualizamos uma tangente de altura zero, obviamente ao buscar o valor no círculo unitário, encontramos que corresponde a zero graus, então:

4 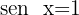
Isolamos a variável x, fazendo uso da propriedade do inverso:
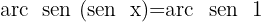
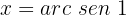
Localizamos na tabela o valor para 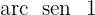
Nos posicionamos no eixo do seno, ou seja, no eixo y, agora localizamos o valor 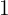 no eixo, e, por fim, nos deslocamos até os pontos que atravessam a circunferência e passam por
no eixo, e, por fim, nos deslocamos até os pontos que atravessam a circunferência e passam por 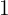 . Esses valores serão o resultado da equação:
. Esses valores serão o resultado da equação:

5 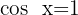
Isolamos a variável x, fazendo uso da propriedade do inverso:
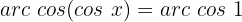
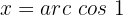
Localizamos na tabela o valor para 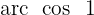
Nos posicionamos no eixo do cosseno, ou seja, no eixo x, agora localizamos o valor 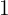 eno eixo, e, por fim, nos deslocamos até os pontos que atravessam a circunferência e passam por
eno eixo, e, por fim, nos deslocamos até os pontos que atravessam a circunferência e passam por 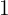 .Esses valores serão o resultado da equação:
.Esses valores serão o resultado da equação:

6 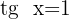
Isolamos a variável x, fazendo uso da propriedade do inverso:

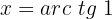
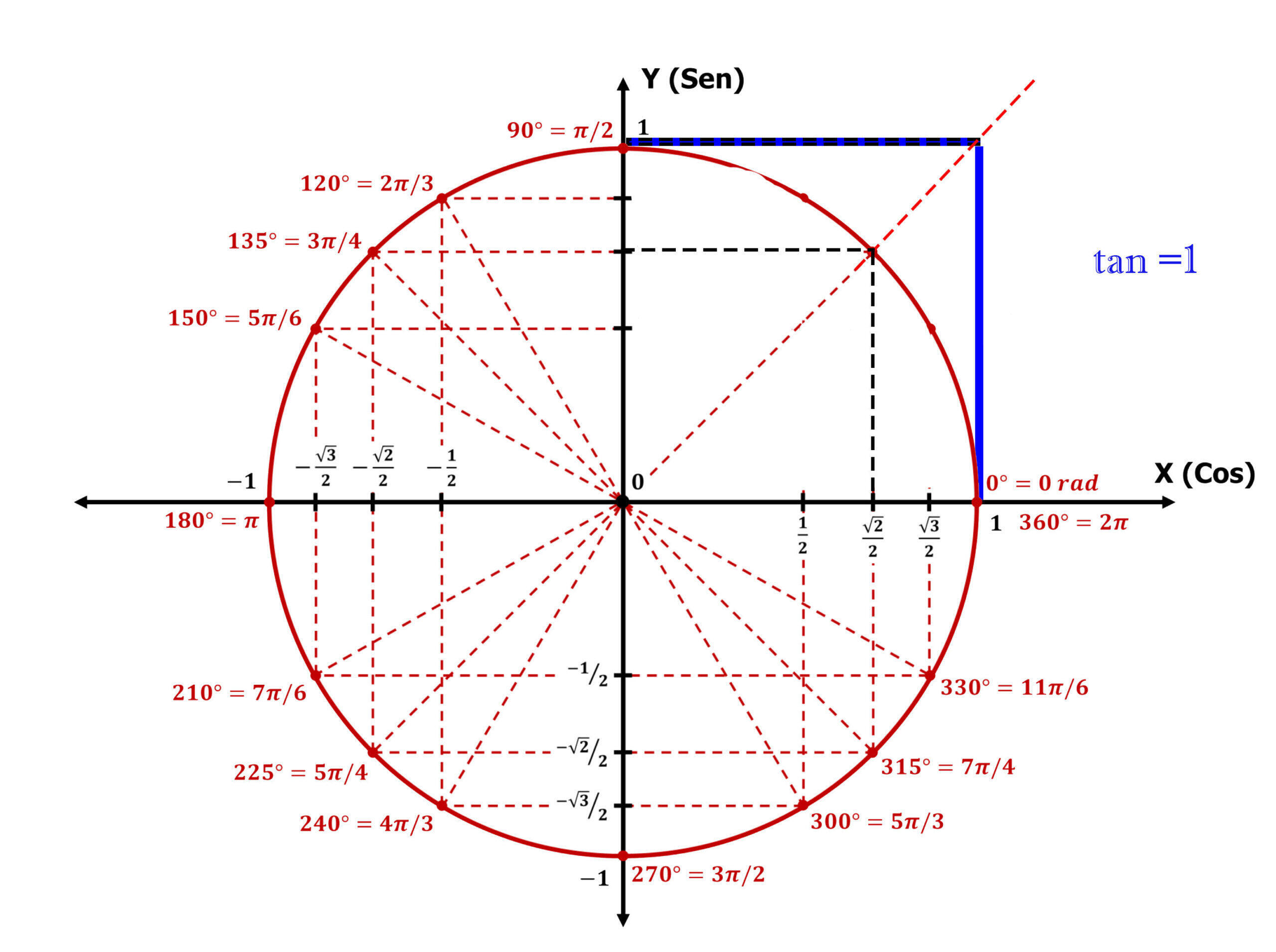
Este exercício foi mostrado no exemplo no início da lição, onde podemos observar a representação gráfica.
Visualizamos uma reta tangente de altura  , traçamos uma linha dessa altura até a origem e observamos o ponto de interseção com a circunferência, buscamos o valor desse ponto no nosso círculo unitário e obtemos o valor da equação:
, traçamos uma linha dessa altura até a origem e observamos o ponto de interseção com a circunferência, buscamos o valor desse ponto no nosso círculo unitário e obtemos o valor da equação:

7 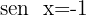
Isolamos a variável x, fazendo uso da propriedade do inverso:
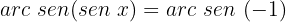
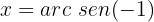
Localizamos na tabela o valor para 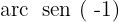
Nos posicionamos no eixo do seno, ou seja, no eixo y, agora localizamos o valor  no eixo, e, por fim, deslocamos até os pontos que atravessam a circunferência e passam por
no eixo, e, por fim, deslocamos até os pontos que atravessam a circunferência e passam por  . Esses valores serão o resultado da equação:
. Esses valores serão o resultado da equação:
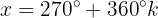
8 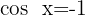
Isolamos a variável x, fazendo uso da propriedade do inverso:
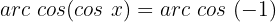

Localizamos na tabela o valor para 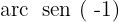
Nos posicionamos no eixo do cosseno, ou seja, no eixo x, agora localizamos o valor  no eixo, e, por fim, deslocamos até os pontos que atravessam a circunferência e passam por
no eixo, e, por fim, deslocamos até os pontos que atravessam a circunferência e passam por  . Esses valores serão o resultado da equação:
. Esses valores serão o resultado da equação:

9 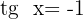
Isolamos a variável x, fazendo uso da propriedade do inverso:
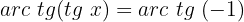 , traçamos uma linha dessa altura até a origem e observamos o ponto de interseção com a circunferência, buscamos o valor desse ponto no nosso círculo unitário e obtemos o valor da equação:
, traçamos uma linha dessa altura até a origem e observamos o ponto de interseção com a circunferência, buscamos o valor desse ponto no nosso círculo unitário e obtemos o valor da equação:
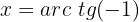
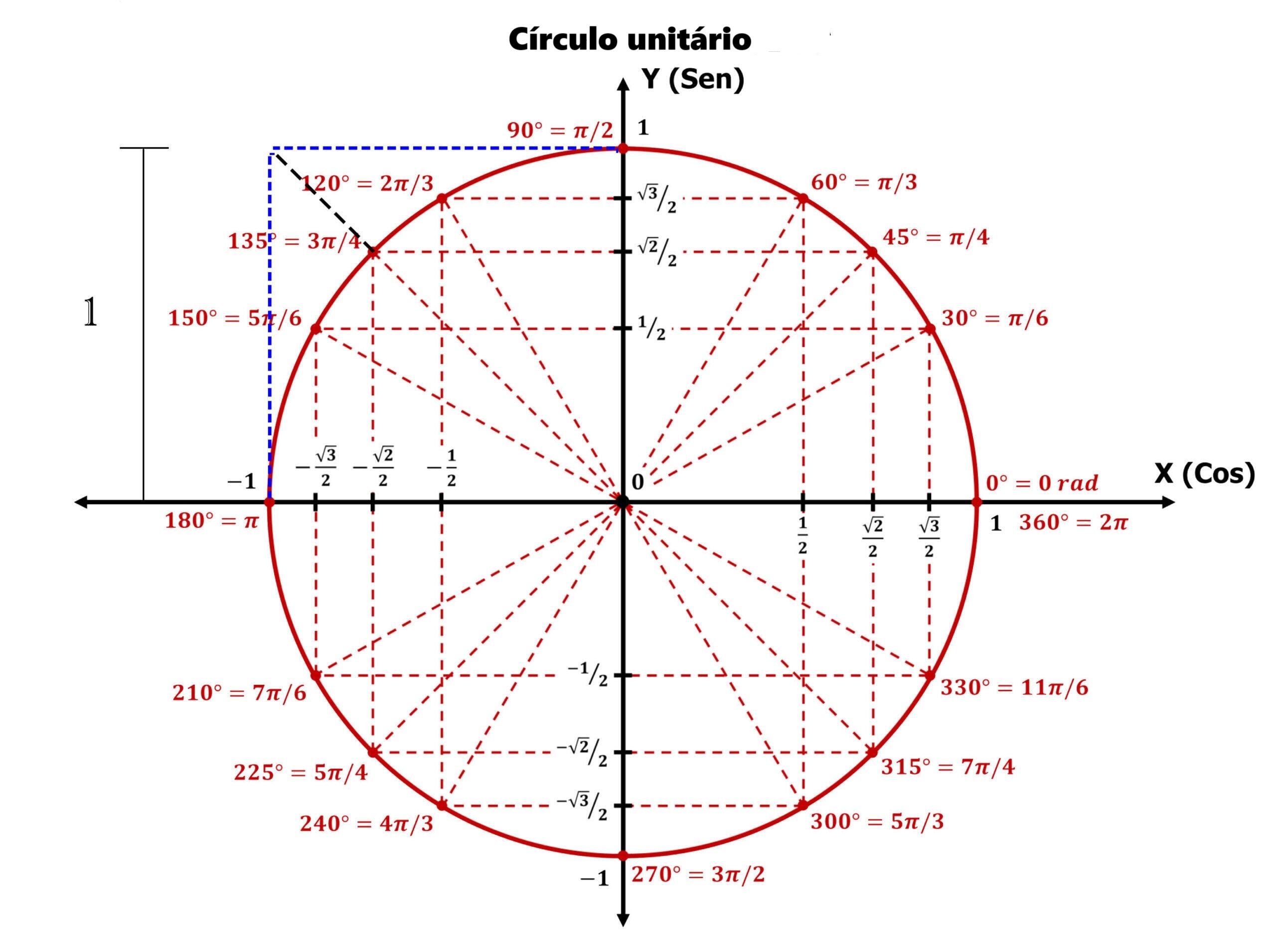
Nos posicionamos na coordenada  , traçamos uma linha dessa altura até a origem e observamos o ponto de interseção com a circunferência, buscamos o valor desse ponto no nosso círculo unitário e obtemos o valor da equação: visualizamos uma reta tangente de altura
, traçamos uma linha dessa altura até a origem e observamos o ponto de interseção com a circunferência, buscamos o valor desse ponto no nosso círculo unitário e obtemos o valor da equação: visualizamos uma reta tangente de altura  , traçamos uma linha dessa altura até a origem e observamos o ponto de interseção com a circunferência, buscamos o valor desse ponto no nosso círculo unitário e obtemos o valor da equação:
, traçamos uma linha dessa altura até a origem e observamos o ponto de interseção com a circunferência, buscamos o valor desse ponto no nosso círculo unitário e obtemos o valor da equação:
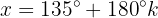
10 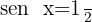
Isolamos a variável x, fazendo uso da propriedade do inverso:

Nos posicionamos no eixo do seno, ou seja, no eixo y, agora localizamos o valor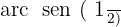 no eixo, e, por fim, nos deslocamos até os pontos que atravessam a circunferência e passam por
no eixo, e, por fim, nos deslocamos até os pontos que atravessam a circunferência e passam por  . Esses valores serão o resultado da equação:
. Esses valores serão o resultado da equação:
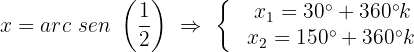
11 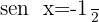
Localizamos na tabela o valor para: 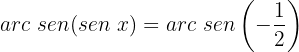
nos posicionamos no eixo do seno, ou seja, no eixo y, agora localizamos o valor 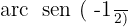 o eixo, e, por fim, nos deslocamos até os pontos que atravessam a circunferência e passam por
o eixo, e, por fim, nos deslocamos até os pontos que atravessam a circunferência e passam por 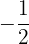 . Esses valores serão o resultado da equação:
. Esses valores serão o resultado da equação:
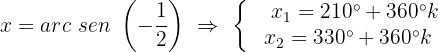
12 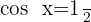
Isolamos a variável x, fazendo uso da propriedade do inverso:
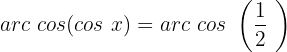
Localizamos na tabela o valor para 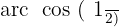
Nos posicionamos no eixo do cosseno, ou seja, no eixo x, agora localizamos o valor  o eixo, e, por fim, nos deslocamos até os pontos que atravessam a circunferência e passam por
o eixo, e, por fim, nos deslocamos até os pontos que atravessam a circunferência e passam por  . Esses valores serão o resultado da equação:
. Esses valores serão o resultado da equação:

13 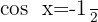
Isolamos a variável x, fazendo uso da propriedade do inverso:

Localizamos na tabela o valor paraa 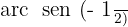
Nos posicionamos no eixo do seno, ou seja, no eixo y, agora localizamos o valor 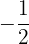 no eixo, e, por fim, nos deslocamos até os pontos que atravessam a circunferência e passam por
no eixo, e, por fim, nos deslocamos até os pontos que atravessam a circunferência e passam por 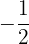 , no eixo, e, por fim, nos deslocamos até os pontos que atravessam a circunferência e passam por
, no eixo, e, por fim, nos deslocamos até os pontos que atravessam a circunferência e passam por

Resolva utilizando as identidades trigonométricas

Para resolver a equação, buscaremos na tabela os valores de 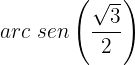

Temos 2 possibilidades. Vamos substituir para a primeiro opção:
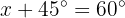
Isolamos a variável:

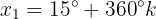
Agora, para a segunda possibilidade. Fazemos a substituição:
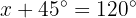
Isolamos a variável:
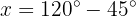
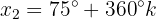

Usando as identidades trigonométricas, vamos simplificar a equação de função a seguir, usando seno, cosseno ou tangente.
Vamos usar a identidade trigonométrica 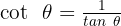
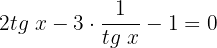
Dessa vez, vamos utilizar a identidade trigonométrica: 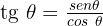
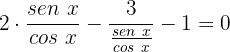
Simplificamos:
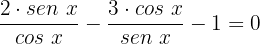
Realizamos a subtração de frações, utilizando o produto cruzado para obter:
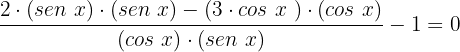
Simplificamos:

Convertemos a unidade em uma fração equivalente com o mesmo denominador:

Substituimos e simplificamos:


Agora multiplicamos ambos os membros da equação por 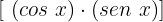
De um lado temos:

Ao simplificar, vamos obter:

Do outro lado, temos:
 lo cual claramente es igual a cero
lo cual claramente es igual a cero
Então:

Vamos a fatorização:
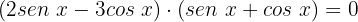
Agora temos 2 possibilidades:
Primeiro caso: isolando o primeiro termo
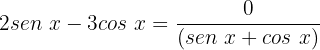

Para este caso, dividiremos ambos os membros por 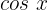


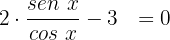
Utilizaremos a identidade 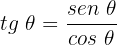
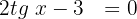
Isolamos a variável:
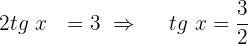
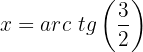
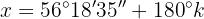
Segundo caso: isolando o segundo termo
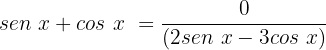

Para este caso, dividiremos ambos membros por 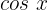
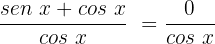
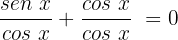

Utilizaremos a identidade 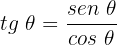

Isolamos a variável:
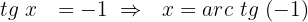
Agora buscamos o valor no nosso círculo unitário, como fizemos anteriormente.

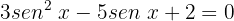
Podemos observar claramente que a equação tem a forma:
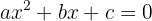
Ou seja, uma equação do segundo grau que pode ser resolvida pela fórmula geral:
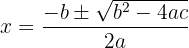
Substituímos:
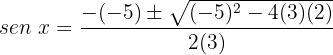
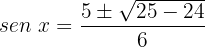
Caso 1:
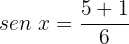
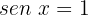
Isolamos a variável:
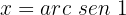
Localizamos o valor no círculo unitário:
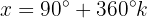
Caso 2:

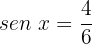
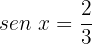
Isolamos a variável:
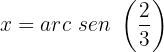
Localizamos o valor no círculo unitário:
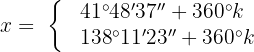
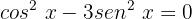
Utilizaremos a identidade trigonométrica fundamental seguinte:

Substituímos na equação:

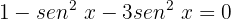
Somamos os termos semelhantes:

Isolamos a variável:
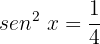
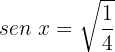
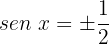
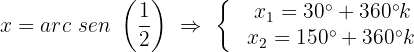
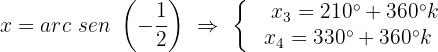
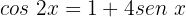
Usaremos a identidade trigonométrica para ângulos duplos:
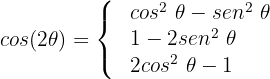
Das 3 opções que temos, utilizaremos a primeira 
Substituímos na nossa equação:
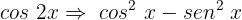
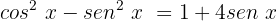
Agora utilizaremos a identidade trigonométrica fundamental seguinte:

Substituímos na equação:

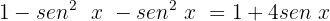
Igualamos a equação a zero e simplificamos os termos semelhantes:

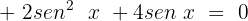
Agora vamos factorar:
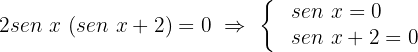
Observamos que geramos 2 casos.
Caso 1:


Caso 2:
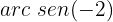
Como podemos observar no círculo unitário, os valores das funções seno e cosseno estão no intervalo [-1,1], então, 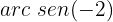
não existe, portanto, este caso não tem solução.
Sem solução.
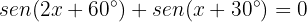
Usaremos a identidade trigonométrica para a soma de ângulos:
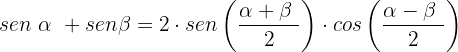
Substituímos os valores do exercício na identidade trigonométrica:

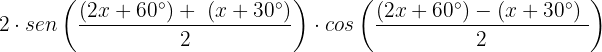
Simplificamos termos semelhantes:

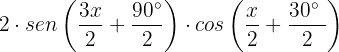
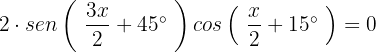
Para que a equação seja igual a zero, é claro que um dos dois termos deve ser igual a zero:
Caso 1: 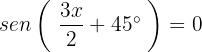
Caso 2: 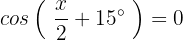
Resolvendo caso 1:
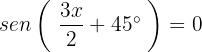
Isolamos a variável e resolvemos a propriedade da função inversa :
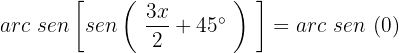
Observando o círculo unitário sabemos que:

Resolvendo a equação para 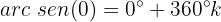
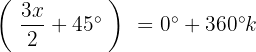
Isolamos a variável e resolvemos:
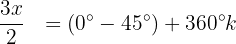
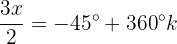
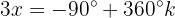
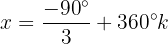

Resolvemos a equação para 
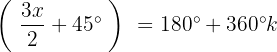
Isolamos a variável e resolvemos:
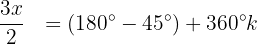

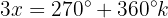
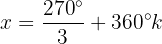
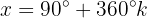
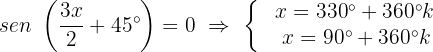
Isso significa que, se a variável x tomar qualquer um desses 2 valores, então a equação 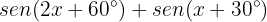 será igual a 0 e, portanto, a equação será satisfeita.
será igual a 0 e, portanto, a equação será satisfeita.
Resolvendo caso 2:

Isolamos a variável aplicando a propriedade da função inversa:
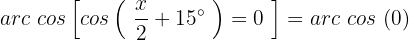
Observando o círculo unitário, sabemos que:

Resolvemos a equação para 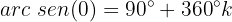

Isolamos a variável e resolvemos:
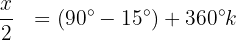


Resolvemos a equação para 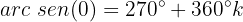
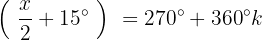
Isolamos a variável e resolvemos:
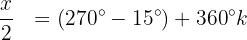
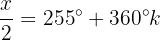

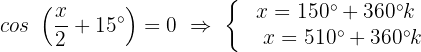
Isso significa que, se a variável x tomar qualquer um desses 2 valores, então a equação 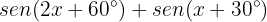
será igual a 0 e, portanto, a equação será satisfeita.
Conclusão:
Os valores que a variável x pode tomar e que são soluções para a equação são:

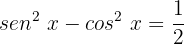
Para este caso, usaremos uma identidade trigonométrica de ângulos duplos:
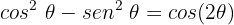
O primeiro passo será multiplicar toda a nossa equação por -1:
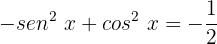
Agora, ordenamos de forma que fique mais parecido com nossa identidade trigonométrica:
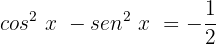
Usamos a identidade, substituindo os valores da nossa equação:
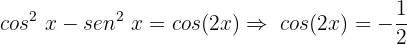
Para isolar a variável, é necessário usar a propriedade da função inversa:
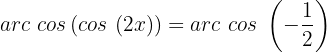

Buscando no círculo unitário, encontraremos que:
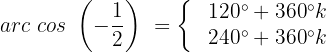
Resolvendo para 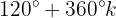 :
:
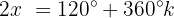
Isolamos a variável:

Resolvendo para 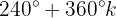 :
:
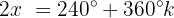
Isolamos a variável:
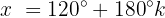
Os valores que a variável x pode tomar e que são soluções para a equação são:

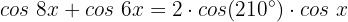
Usaremos a identidade trigonométrica da soma de cossenos:
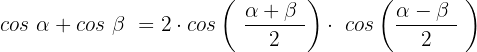
Substituímos:
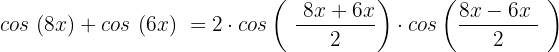

A equação fica da seguinte forma:
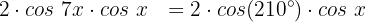
Dividimos ambos os lados da equação por 2:
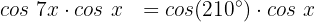
Dividimos ambos os lados da equação por cos(x):
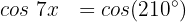
Aplicamos a propriedade da função inversa:

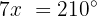
Isolamos a variável:

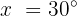
A equação é satisfeita quando 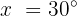
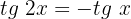
Para este caso, utilizaremos a identidade trigonométrica localizada na seção de "Identidades trigonométricas para ângulos duplos":

Vamos substituir com os valores da nossa equação para obter:

Então, nossa equação ficará da seguinte forma:
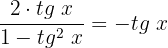
Igualaremos a equação a zero:
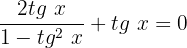
Realizamos a soma das frações usando o produto cruzado:
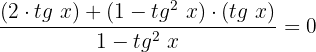
Eliminamos o denominador multiplicando ambos os lados da equação por 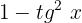 :
:
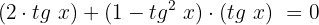
Realizamos o produto indicado:
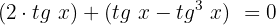
Agrupamos termos semelhantes e os somamos:
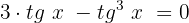
Fatoramos usando  como fator comum:
como fator comum:

Agora, dividimos ambos os lados da equação por  e obtemos:
e obtemos:
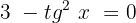
Multiplicamos por -1 ambos os lados da equação e ordenamos para resolver como uma equação de segundo grau:

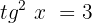
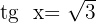
Aplicamos a propriedade da função inversa:
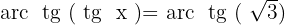
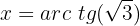
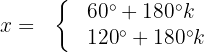

Primeiro, subtraímos  de ambos os lados:
de ambos os lados:
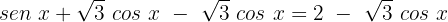
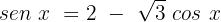
Agora, elevamos ambos os lados ao quadrado:
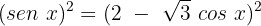
Igualamos a equação a zero:
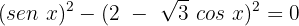
Resolvemos os quadrados, para o que usamos a fórmula do binômio ao quadrado:
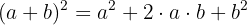

Utilizamos a identidade trigonométrica fundamental.

Substituimos

Simplificamos:


Simplificamos os termos semelhantes:

Fazemos uma substituição de variável:
Seja 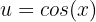
Substituimos:
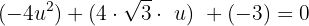
Observamos que trata-se de uma equação do segundo grau que podemos resolver pela fórmula geral:
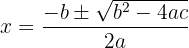
Substituimos:
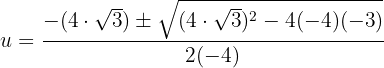
Resolvemos:
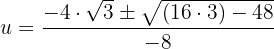

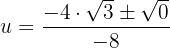
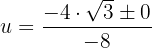
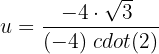

Desfazemos a substituição de variável:
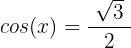
Aplicamos a propriedade da função inversa:
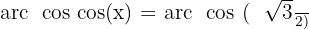

Agora, devemos apenas localizar o valor na na tabela do círculo unitário:
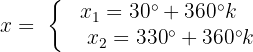
A equação é satisfeita quando x assume qualquer um desses 2 valores.

Para este caso, utilizaremos a identidade trigonométrica para ângulos duplos:
Buscamos no círculo unitário o valor correspondente a 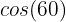 :
:

Substituimos:
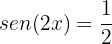
Aplicamos a propriedade da função inversa:
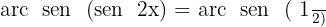
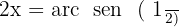
Localizamos os valores correspondentes no círculo unitário:
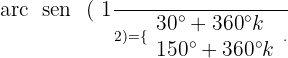
Portanto:

Isolamos a variável dividindo por 2:
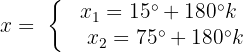
A equação é satisfeita quando x assume qualquer um desses 2 valores.

Usaremos la siguiente identidad trigonométrica para ángulos dobles:
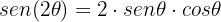
Antes de fazer a substituição, vamos obteruma variante dividindo por 2 cada lado de la identidade:
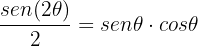
Substituimos:
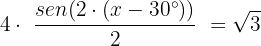
Simplificamos realizando a divisão indicada:

Dividimos ambos lados por 2:

Aplicamos a propeiedade de função inversa:
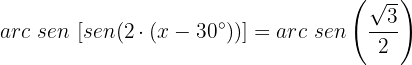
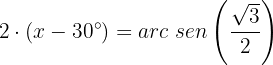
Localizamos o valor para 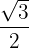 no círculo unitário:
no círculo unitário:

Substituimos para ambos casos:
Caso 1:
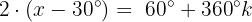
Dividimos ambos lados por 2:
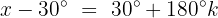
Isolamos a variável, somando 30° em ambos os lados da equação:
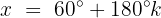
Caso 2:
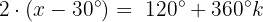
Dividimos ambos lados por 2:
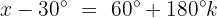
Isolamos a variável, somando 30° em ambos os lados da equação:
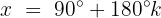
A equação é satifeita quando:
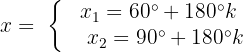
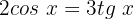
utilizaremos a identidade trigonométrica básica:

Substituimos:
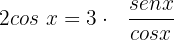

Eliminamos o denominador multiplicando ambos os lados da equação por 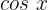
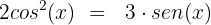
Agora, utilizaremos a identidade trigonométrica fundamental:
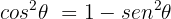
Substituimos:

Aplicamos a distributiva:

Igualamos a zero e ordenamos:
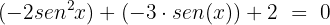
Multiplicamos toda a expressão por 
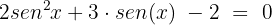
Realizamos uma substituição de variável, onde:
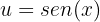
Substituimos:

Resolvemos pela fórmula geral para equações do segundo grau:


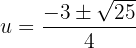

Desfazemos a substituição de variável:
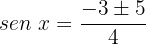
Caso 1:

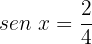
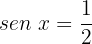
Aplicamos a propriedade da função inversa:
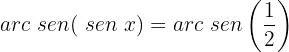
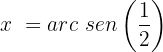
Localizamos o valor correspondente no círculo unitário:
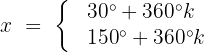
Caso 2:
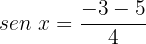
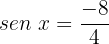
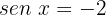
Aplicamos a propriedade da função inversa:
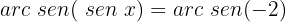
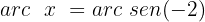
Como sabemos e podemos observar no círculo unitário, a função seno não está definida para valores maiores que 1, nem menores que -1, portanto este caso não tem solução.
A equação é satisfeita quando:
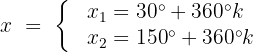

Usaremos a identidade trigonométrica para ângulos duplos:
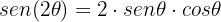
Substituimos:

Portanto:

Simplificamos:
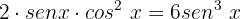
Igualamos a equação a zero:
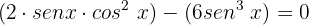
Fatoramos:
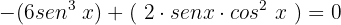
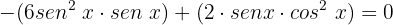
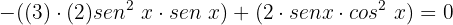
Extraímos o termo comum 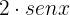 :
:
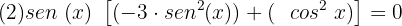
Agora vamos fatorar a parte dentro do colchete:
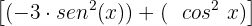
Reescrevemos o 3 como 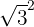
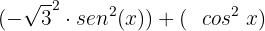
Ordenamos para poder aplicar a diferença de quadrados:
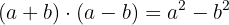

Aplicamos a lei dos sinais  :
:
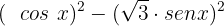
Agora podemos aplicar a diferença de quadrados:
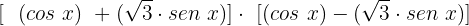
Lembre-se que este é o resultado da parte do colchete que tínhamos acima, vamos substituí-la na nossa equação agora que já está fatorada:

É claro que, para que a equação seja satisfeita, basta que um dos colchetes dê como resultado zero. Então, temos 3 casos:
Caso 1, quando 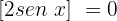
Dividimos por 2 ambos os membros da equação:
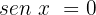
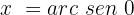
Localizamos no círculo unitário:
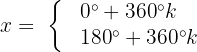
Caso 2, quando 
Dividimos ambos os membros por cos x e usamos a identidade trigonométrica básica da tangente:
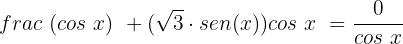
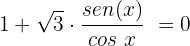
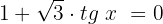
Isolamos a variável:
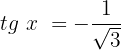
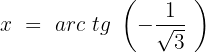

Caso 3, quando 
Este caso é bem semelhante ao Caso 2:
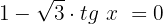
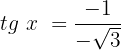
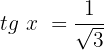
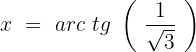

A equação é satisfeita quando x assume um dos seguintes valores:


Igualamos a equação a zero:
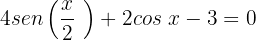
Aplicamos uma substituição de variável, onde 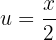
Substituimos:

Usamos a seguinte identidade trigonométrica para ângulos duplos:
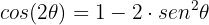
Substituímos a variável na identidade:
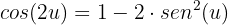
Substituímos o que obtivemos na nossa equação:

Desenvolvemos:
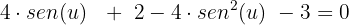
Somamos termos semelhantes e ordenamos:
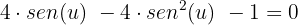
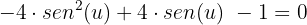
Realizamos outra substituição de variável, seja 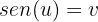
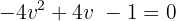
Resolvemos pela fórmula geral para equações do segundo grau:
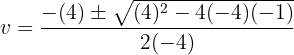

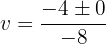
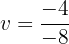
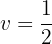
Desfazemos a última substituição de variável:
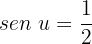
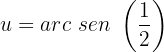
Localizamos os valores no círculo unitário e temos que:
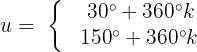
Agora, desfazemos a primeira substituição de variável:
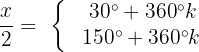
Isolamos a variável, multiplicando por 2:
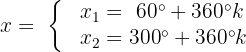
A equação é satisfeita quando x assume qualquer um desses 2 valores.
Resumir com IA:












