Bem-vindo ao fascinante mundo da elipse, uma figura geométrica que tem encantado matemáticos e cientistas por séculos. Nesta coleção de exercícios e problemas, você explorará os segredos e as propriedades da elipse.
A elipse é muito mais do que uma simples forma ovalada. Trata-se de uma curva com propriedades únicas que a tornam indispensável em diversas áreas do conhecimento. Através desses desafios, você se aprofundará no estudo de sua equação, seus elementos característicos como os focos e vértices e as relações entre seus diferentes parâmetros.
Seja você um estudante que está começando a se familiarizar com o mundo da elipse ou um entusiasta de matemática em busca de desafios mais complexos, esta coleção fornecerá uma base sólida para compreender e aplicar os princípios da elipse em diversas situações. Prepare-se para aprimorar seu raciocínio analítico!

Elementos da elipse
Represente graficamente e determine as coordenadas dos focos, dos vértices e a excentricidade das seguintes elipses.
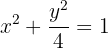
1 Eixo maior
A equação da elipse já está na forma canônica, então podemos calcular o valor do semi-eixo maior:

Com isso, podemos encontrar os vértices que formam o eixo maior:

2 Eixo menor
O valor do semi-eixo menor é:

Portanto, os vértices que estão no eixo menor são:

3 Focos
Agora, vamos calcular o valor da distância semifocal:

Com esse valor, podemos localizar os focos da elipse:

4 Excentricidade
A excentricidade da elipse é o quociente entre a distância semifocal e o semi-eixo maior:
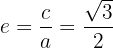
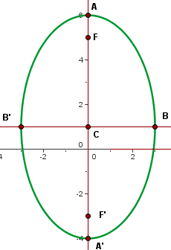
5 Gráfico
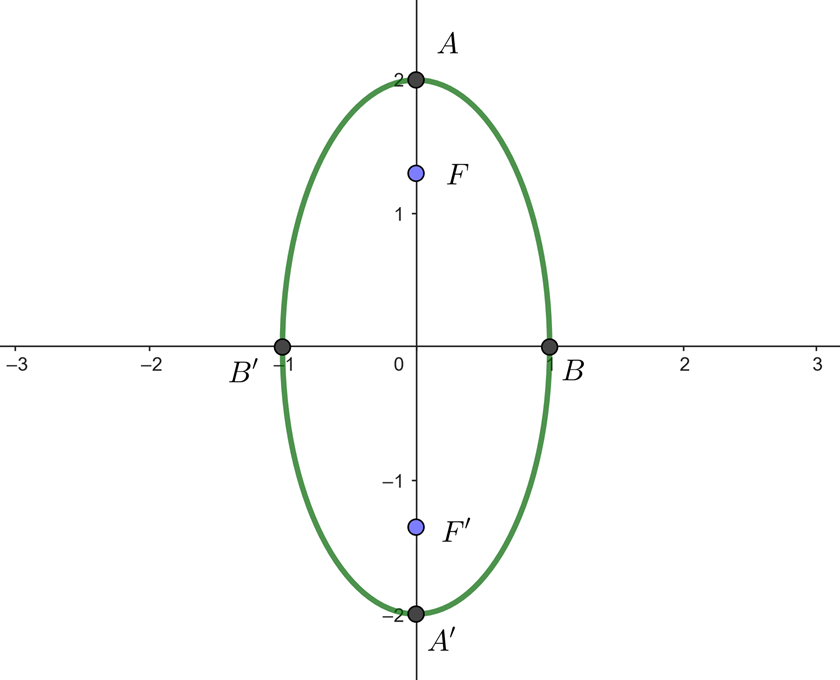

1 Eixo maior
A equação da elipse já está na forma canônica, então podemos calcular o valor do semi-eixo maior:

Com isso, podemos encontrar os vértices que formam o eixo maior:

2 Eixo menor
O valor do semi-eixo menor é:

Portanto, os vértices que estão no eixo menor são:

3 Focos
Agora, vamos calcular o valor da distância semifocal:

Com esse valor, podemos localizar os focos da elipse:

4 Excentricidade
A excentricidade da elipse é o quociente entre a distância semifocal e o semi-eixo maior:

5 Gráfico
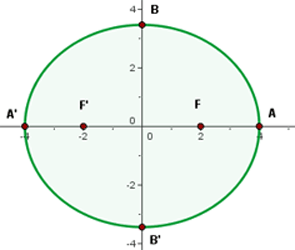
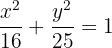
1 Eixo maior
A equação da elipse já está na forma canônica, então podemos calcular o valor do semi-eixo maior:

Com isso, podemos encontrar os vértices que formam o eixo maior:

2 Eixo menor
O valor do semi-eixo menor é:

Portanto, os vértices que estão no eixo menor são:

3 Focos
Agora, vamos calcular o valor da distância semifocal:

Com esse valor, podemos localizar os focos da elipse:

4 Excentricidade
A excentricidade da elipse é o quociente entre a distância semifocal e o semi-eixo maior:
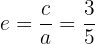
5 Gráfico
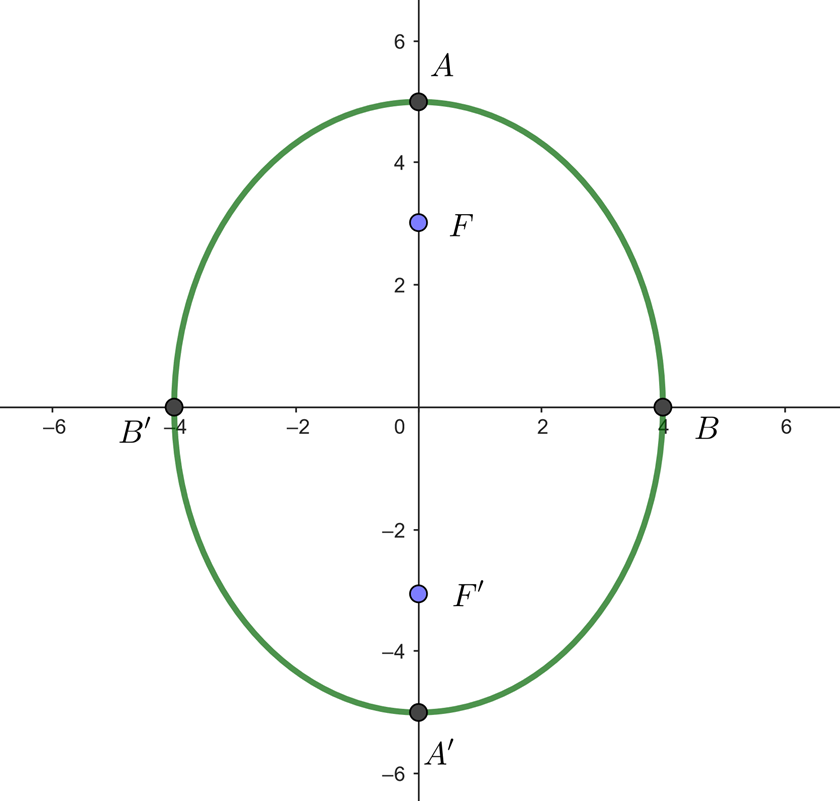

1 Obter equação canônica (reduzida)

2 Eixo maior
Obtemos o valor do semieixo maior

E encontrar os vértices que formam o eixo maior:

3 Eixo menor
O valor do semi-eixo menor é:

Portanto, os vértices que estão no eixo menor são:

4 Focos
Agora, vamos calcular o valor da distância semifocal:

Com esse valor, podemos localizar os focos da elipse:

5 Excentricidade
A excentricidade da elipse é o quociente entre a distância semifocal e o semi-eixo maior:
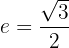
6 Gráfico
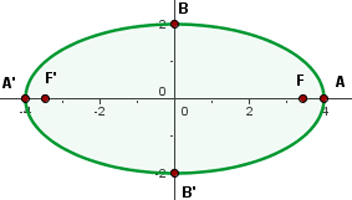
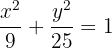
1 Eixo maior
A equação da elipse já está na forma canônica, então procedemos para obter o valor do semi-eixo maior:

E assim, encontramos os vértices que formam o eixo maior:

2 Eixo menor
O valor do semi-eixo menor é:

Portanto, os vértices que se encontram no eixo menor são:

3 Focos
Agora, calculamos o valor da distância semifocal:

E com isso, localizamos os focos:

4 Excentricidade
A excentricidade é igual ao quociente da distância semifocal e o semi-eixo maior:

5 Gráfico
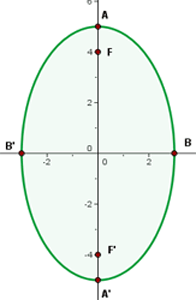
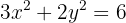
1 Obter a equação canônica (reduzida)

2 Eixo maior
A equação da elipse já está na forma canônica, então procedemos para obter o valor do semi-eixo maior:

E assim, encontramos os vértices que formam o eixo maior:

3 Eixo menor
O valor do semi-eixo menor é:

Portanto, os vértices que se encontram no eixo menor são:

4 Focos
Agora, calculamos o valor da distância semifocal:

E com isso, localizamos os focos:

5 Excentricidade
A excentricidade é igual ao quociente da distância semifocal e o semi-eixo maior:

6 Gráfico
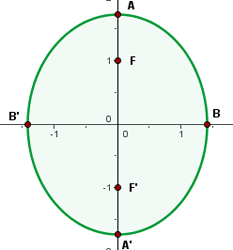
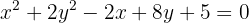
1 Obter a equação canônica (reduzida)
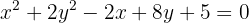
Completamos o quadrado perfeito:
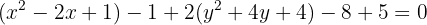
Substituímos os trinomios pelos binômios ao quadrado:
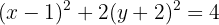
Dividimos tudo por 4:
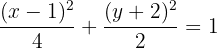
2 Centro
A partir da equação da elipse canônica, encontramos o centro:
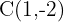
3 Eixo maior
A equação da elipse já está na forma canônica, então procedemos para obter o valor do semi-eixo maior:

E assim, encontramos os vértices que formam o eixo maior:

4 Eixo menor
O valor do semi-eixo menor é:

Portanto, os vértices que se encontram no eixo menor são:

5 Focos
Agora, calculamos o valor da distância semifocal:

E com isso, localizamos os focos:

6 Gráfico
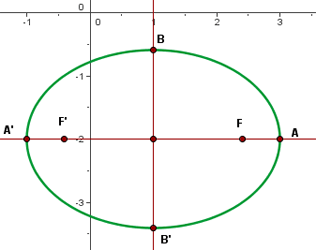

1 Obter a equação canônica (reduzida)

Completamos o quadrado perfeito:
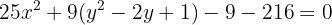
Substituímos os trinomios pelos binômios ao quadrado:
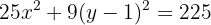
Dividimos tudo por 225:
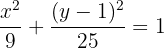
2 Centro
A partir da equação da elipse canônica, encontramos o centro:
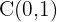
3 Eixo maior
A equação da elipse já está na forma canônica, então procedemos para obter o valor do semi-eixo maior:

E assim, encontramos os vértices que formam o eixo maior:

4 Eixo menor
O valor do semi-eixo menor é:

Portanto, os vértices que se encontram no eixo menor são:

5 Focos
Agora, calculamos o valor da distância semifocal:

E com isso, localizamos os focos:

6 Gráfico

1 Obter a equação canônica

Completamos o quadrado perfeito:
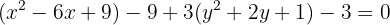
Substituímos os trinomios pelos binômios ao quadrado:
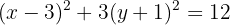
Dividimos tudo por 12:
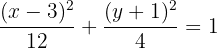
2 Centro
A partir da equação da elipse canônica, encontramos o centro:
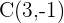
3 Eixo maior
A equação da elipse já está na forma canônica, então procedemos para obter o valor do semi-eixo maior:

E assim, encontramos os vértices que formam o eixo maior:

4 Eixo menor
O valor do semi-eixo menor é:

Portanto, os vértices que se encontram no eixo menor são:

5 Focos
Agora, calculamos o valor da distância semifocal:

E com isso, localizamos os focos:

6 Gráfico
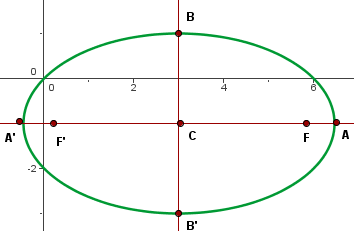
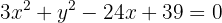
1 Obter a equação canônica
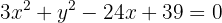
Completamos o quadrado perfeito:

Substituímos os trinomios pelos binômios ao quadrado:
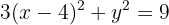
Dividimos tudo por 9:
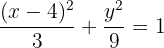
2 Centro
A partir da equação da elipse canônica, encontramos o centro:

3 Eixo maior
A equação da elipse já está na forma canônica, então procedemos para obter o valor do semi-eixo maior:

E assim, encontramos os vértices que formam o eixo maior:

4 Eixo menor
O valor do semi-eixo menor é:

Portanto, os vértices que se encontram no eixo menor são:

5 Focos
Agora, calculamos o valor da distância semifocal:

E com isso, localizamos os focos:

6 Gráfico
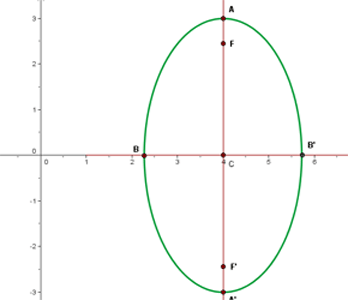
Equação da elipse
Determine a equação da elipse sabendo:
a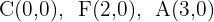
b
c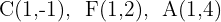
d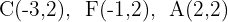
a 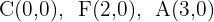
O valor de  a distância do centro até o vértice A, enquanto o valor
a distância do centro até o vértice A, enquanto o valor  é a distância do centro até o foco. Então:
é a distância do centro até o foco. Então:

Os valores  ,
,  e
e  têm uma relação que é análoga ao Teorema de Pitágoras, ou seja:
têm uma relação que é análoga ao Teorema de Pitágoras, ou seja:
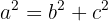
Isolamos para calcular o valor de 


Concluímos que:
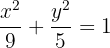
b 
O valor de  é a distância do centro até o vértice A, enquanto o valor de
é a distância do centro até o vértice A, enquanto o valor de  é a distância do centro até o foco. Então:
é a distância do centro até o foco. Então:

Os valores  ,
,  e
e  têm uma relação que é análoga ao Teorema de Pitágoras, ou seja:
têm uma relação que é análoga ao Teorema de Pitágoras, ou seja:
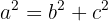
Isolamos para calcular o valor de 

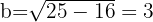
Concluímos que:
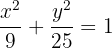
c 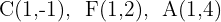
O valor de  a distância do centro até o vértice A, enquanto o valor de
a distância do centro até o vértice A, enquanto o valor de  é a distância do centro até o foco. Então:
é a distância do centro até o foco. Então:

Os valores  ,
,  e
e  têm uma relação que é análoga ao Teorema de Pitágoras, ou seja:
têm uma relação que é análoga ao Teorema de Pitágoras, ou seja:
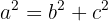
Isolamos para calcular o valor de 

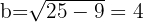
Concluímos que:
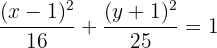
d 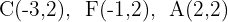
O valor de  é a distância do centro até o vértice A, enquanto o valor de
é a distância do centro até o vértice A, enquanto o valor de  é a distância do centro até o foco. Então:
é a distância do centro até o foco. Então:

Os valores  ,
,  e
e  têm uma relação que é análoga ao Teorema de Pitágoras, ou seja:
têm uma relação que é análoga ao Teorema de Pitágoras, ou seja:
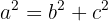
Isolamos para calcular o valor de 

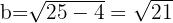
Concluímos que:
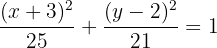
Escreva a equação canônica da elipse com centro na origem que passa pelo ponto 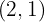 , cujo eixo menor tem comprimento
, cujo eixo menor tem comprimento  e está sobre o eixo
e está sobre o eixo 
O eixo menor tem comprimento 

A equação canônica da elipse com centro na origem e com o eixo menor sobre o eixo Y tem a forma:
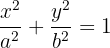
Como o ponto (2,1) pertence à elipse, suas coordenadas devem satisfazer a equação canônica da elipse. Ou seja:

Isolando para encontrar o valor de 

Conhecendo os valores de  e
e  , concluimos que:
, concluimos que:
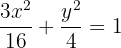
A distância focal de uma elipse com centro na origem é  . . Um ponto da elipse está a
. . Um ponto da elipse está a  e
e  de distância dos seus focos, respectivamente. Calcule a equação canônica dessa elipse se o eixo maior estiver sobre o eixo
de distância dos seus focos, respectivamente. Calcule a equação canônica dessa elipse se o eixo maior estiver sobre o eixo 
A distância focal é dada por 

Lembre-se de que a soma das distâncias de um ponto na elipse aos focos é igual a 

Os valores  ,
,  e
e  têm uma relação que é análoga ao Teorema de Pitágoras, ou seja:
têm uma relação que é análoga ao Teorema de Pitágoras, ou seja:
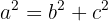
Isolando para calcular o valor de 

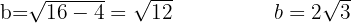
Conhecendo os valores de  e
e  , concluimos que:
, concluimos que:

Escreva a equação canônica da elipse que passa pelos pontos:

Como passa pelos pontos  , suas coordenadas devem satisfazer a equação canônica da elipse. Ou seja, temos o sistema:
, suas coordenadas devem satisfazer a equação canônica da elipse. Ou seja, temos o sistema:
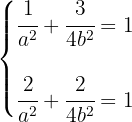
Resolvendo o sistema:
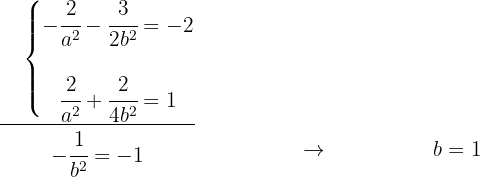
Portanto:
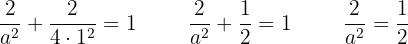
Isolamos 

Por fim:
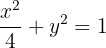
Determine a equação canônica de uma elipse com centro na origem e eixo maior sobre o eixo  , cuja distância focal é
, cuja distância focal é  e a área do retângulo formado pelos eixos (maior e menor) é
e a área do retângulo formado pelos eixos (maior e menor) é 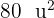
Como os lados do retângulo são os eixos da elipse e medem  e
e  então:
então:
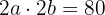
A distância focal é de 

Os valores  ,
,  e
e  têm uma relação que é análoga ao Teorema de Pitágoras, ou seja,
têm uma relação que é análoga ao Teorema de Pitágoras, ou seja,

Isso nos dá o sistema de duas equações:
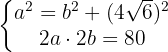
Da primeira equação, isolamos  e da segunda,
e da segunda, 
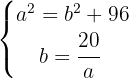
Usamos  da segunda equação para substituir na primeira equação:
da segunda equação para substituir na primeira equação:
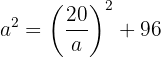
Desenvolvemos a equação:
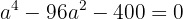
Resolvemos usando a fórmula geral e obtemos o valor de 

Conhecendo os valores de  e
e  , concluimos que:
, concluimos que:

Coordenadas de cordas da elipse
Encontre as coordenadas da corda que intercepta a reta: na elipse de equação:
na elipse de equação: 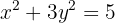
1 Encontre os pontos de interseção
Os pontos de interseção são aqueles que resolvem o sistema das equações da reta e da elipse.
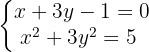
Para resolver, podemos isolar  da primeira equação e elevar ao quadrado. Também isolamos
da primeira equação e elevar ao quadrado. Também isolamos 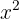 da segunda equação:
da segunda equação:
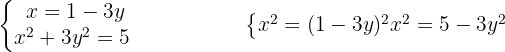
Igualamos ambas as equações:
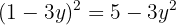
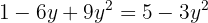
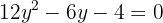
Usamos a fórmula geral para encontrar as soluções:
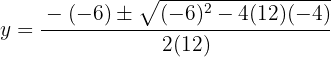
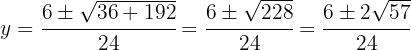
As soluções para a coordenada  são:
são:

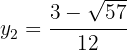
As coordenadas  podem ser calculadas usando qualquer equação do sistema. Neste caso, vamos usar:
podem ser calculadas usando qualquer equação do sistema. Neste caso, vamos usar:
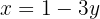
Portanto, os pontos de interseção são dados por:
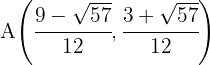

Encontre as coordenadas da corda que intercepta a reta:  na elipse de equação:
na elipse de equação: 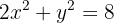
1 Encontre os pontos de interseção
Os pontos de interseção são aqueles que resolvem o sistema das equações da reta e da elipse.
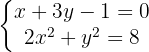
Para resolver, podemos isolar  a primeira equação e elevar ao quadrado. Também isolamos
a primeira equação e elevar ao quadrado. Também isolamos 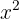 da segunda equação.
da segunda equação.

Igualamos ambas as equações:
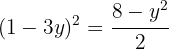
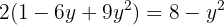
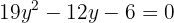
Usamos a fórmula geral para encontrar as soluções:
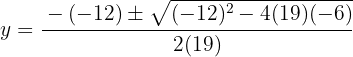
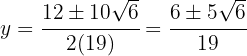
As soluções para a coordenada  são:
são:
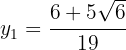
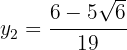
As coordenadas  podem ser calculadas usando qualquer equação do sistema. Neste caso, vamos usar:
podem ser calculadas usando qualquer equação do sistema. Neste caso, vamos usar:
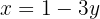
Portanto, os pontos de interseção são dados por:
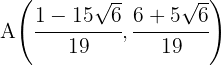
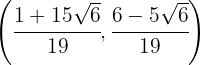
Encontre as coordenadas da corda que intercepta a reta: 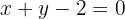 na elipse de equação:
na elipse de equação: 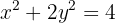
1 Encontre os pontos de interseção
Os pontos de interseção são aqueles que resolvem o sistema das equações da reta e da elipse.
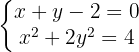
Para resolver, podemos isolar  a primeira equação e elevar ao quadrado. Também isolamos
a primeira equação e elevar ao quadrado. Também isolamos 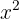 da segunda equação.
da segunda equação.

Igualamos ambas as equações:
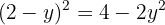
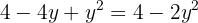
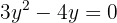
Usamos a fórmula geral para encontrar as soluções:
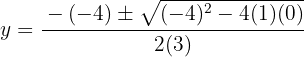
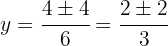
As soluções para a coordenada  são:
são:
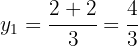
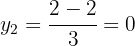
As coordenadas  podem ser calculadas usando qualquer equação do sistema. Neste caso, vamos usar:
podem ser calculadas usando qualquer equação do sistema. Neste caso, vamos usar:
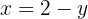
Portanto, os pontos de interseção são dados por:
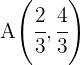
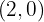
Encontre as coordenadas da corda que intercepta a reta: 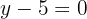 na elipse de equação:
na elipse de equação: 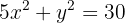
1 Encontre os pontos de interseção
Os pontos de interseção são aqueles que resolvem o sistema das equações da reta e da elipse.
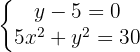
Para resolver, podemos isolar  da primeira equação e substituir na segunda equação:
da primeira equação e substituir na segunda equação:
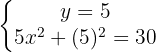
E obtemos 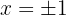
Assim, os pontos de interseção são dados por:
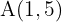
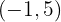
Encontre as coordenadas do ponto médio da corda que intercepta a reta: 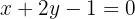 na elipse da equação:
na elipse da equação: 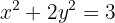
1 Encontre pontos de interseção
Os pontos de interseção são aqueles que resolvem o sistema das equações da reta e da elipse.
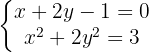
Para resolver, podemos isolar  da primeira equação e elevar ao quadrado. Também isolamos
da primeira equação e elevar ao quadrado. Também isolamos 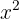 da segunda equação.
da segunda equação.

Igualamos ambas as equações:
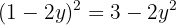
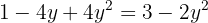

Usamos a fórmula geral para encontrar as soluções:
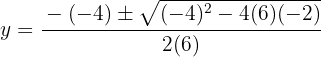
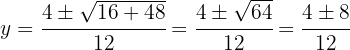
As soluções para a coordenada são:
são:
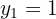
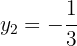
As coordenadas  podem ser calculadas usando qualquer equação do sistema. Neste caso, vamos usar:
podem ser calculadas usando qualquer equação do sistema. Neste caso, vamos usar:
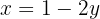
Portanto, os pontos de interseção são dados por:
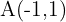
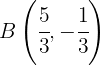
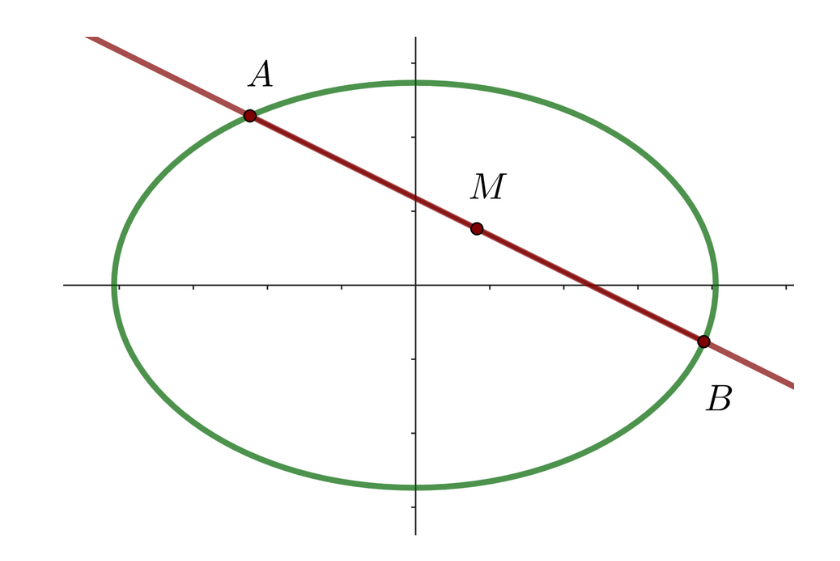
2 Encontre o ponto médio
O ponto médio entre os pontos A e B é dado por:

Resumir com IA:












