Encontre o desvio médio, a variância e o desvio padrão das seguintes séries de números:
a)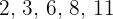 
.
b)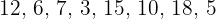 
.
a) Para a série de números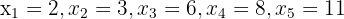 
com 
temos os seguintes cálculos.
Para o desvio médio, primeiro precisamos calcular o valor da média.
Média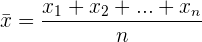
Em seguida calculamos o valor de desvio médio.
Desvio médio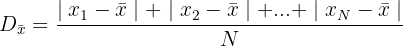
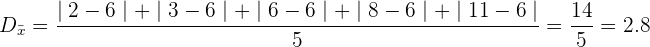
Agora, calculamos o valor da variância.
Variância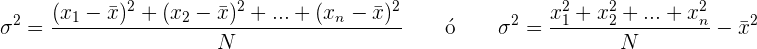
E, finalmente, calculamos o valor de desvio padrão.
Desvio padrão
b) Para a série de números 
com 
temos os seguintes cálculos.
Para o desvio médio, primeiro precisamos calcular o valor da média.
Média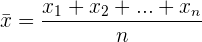
Em seguida, calculamos o valor de desvio médio.
Desvio médio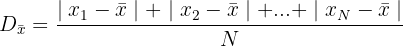
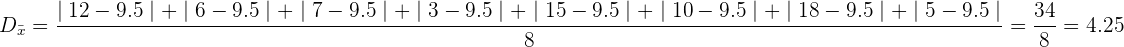
Agora, calculamos o valor da variância.
Variância
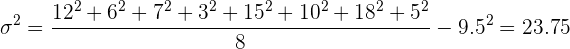
E, finalmente, calculamos o valor do desvio padrão.
Desvio padrão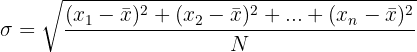
Um pediatra obteve a seguinte tabela com os meses de idade de 50 crianças que foram consultadas quando andaram pela primeira vez. Calcule a variância.
| Meses | Crianças |
|---|---|
| 9 | 1 |
| 10 | 4 |
| 11 | 9 |
| 12 | 16 |
| 13 | 11 |
| 14 | 8 |
| 15 | 1 |
Completamos a tabela com:
a) O produto da variável pela sua frequência absoluta (xi · fi) para calcular a média.
b) O produto da variável ao quadrado pela sua frequência absoluta (xi² · fi) para calcular a variância e o desvio padrão.
| xi | fi | xi · fi | x²i · fi |
|---|---|---|---|
| 9 | 1 | 9 | 81 |
| 10 | 4 | 40 | 400 |
| 11 | 9 | 99 | 1089 |
| 12 | 16 | 192 | 2304 |
| 13 | 11 | 143 | 1859 |
| 14 | 8 | 112 | 1568 |
| 15 | 1 | 15 | 225 |
| 50 | 610 | 7526 |
Média aritmética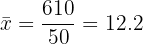
Variância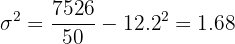
O resultado de lançar dois dados 120 vezes está na seguinte tabela. Calcule a variância.
| Somas | Vezes |
|---|---|
| 2 | 3 |
| 3 | 8 |
| 4 | 9 |
| 5 | 11 |
| 6 | 20 |
| 7 | 19 |
| 8 | 16 |
| 9 | 13 |
| 10 | 11 |
| 11 | 6 |
| 12 | 4 |
Adicionamos as colunas de xi · fi e de xi² · fi
| xi | fi | xi · fi | xi² · fi |
|---|---|---|---|
| 2 | 3 | 6 | 12 |
| 3 | 8 | 24 | 72 |
| 4 | 9 | 36 | 144 |
| 5 | 11 | 55 | 275 |
| 6 | 20 | 120 | 720 |
| 7 | 19 | 133 | 931 |
| 8 | 16 | 128 | 1024 |
| 9 | 13 | 117 | 1053 |
| 10 | 11 | 110 | 1100 |
| 11 | 6 | 66 | 726 |
| 12 | 4 | 48 | 576 |
| 120 | 843 | 6633 |
Média aritmética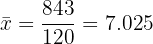
Variância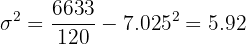
Calcule a variância de uma distribuição estatística que está dada na seguinte tabela.
| fi | |
|---|---|
| [10, 15) | 3 |
| [15, 20) | 5 |
| [20, 25) | 7 |
| [25, 30) | 4 |
| [30, 35) | 2 |
Adicionamos as colunas de xi · fi e de xi² · fi
| xi | fi | xi · fi | xi² · fi | |
|---|---|---|---|---|
| [10, 15) | 12.5 | 3 | 37.5 | 468.75 |
| [15, 20) | 17.5 | 5 | 87.5 | 1531.25 |
| [20, 25) | 22.5 | 7 | 157.5 | 3543.75 |
| [25, 30) | 27.5 | 4 | 110 | 3025 |
| [30, 35) | 32.5 | 2 | 65 | 2112.5 |
| 21 | 457.5 | 10681.25 |
Resultado:
Média
Variância
Calcule a variância da distribuição da seguinte tabela.
| xi | fi | xi · fi | xi² · fi | |
|---|---|---|---|---|
| [10, 20) | 15 | 1 | 15 | 225 |
| [20, 30) | 25 | 8 | 200 | 5000 |
| [30,40) | 35 | 10 | 350 | 12 250 |
| [40, 50) | 45 | 9 | 405 | 18 225 |
| [50, 60) | 55 | 8 | 440 | 24 200 |
| [60,70) | 65 | 4 | 260 | 16 900 |
| [70, 80) | 75 | 2 | 150 | 11 250 |
| 42 | 1 820 | 88 050 |
Média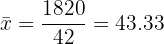
Variância
As alturas dos jogadores de uma equipe de basquete estão dadas na tabela. Calcule a variância.
| Altura | Nº de jogadores |
|---|---|
| [1.70, 1.75) | 1 |
| [1.75, 1.80) | 3 |
| [1.80, 1.85) | 4 |
| [1.85, 1.90) | 8 |
| [1.90, 1.95) | 5 |
| [1.95, 2.00) | 2 |
Completamos a tabela com as colunas de xi · fi e de xi² · fi
| xi | fi | Fi | xi · fi | xi² · fi | |
|---|---|---|---|---|---|
| [1.70, 1.75) | 1.725 | 1 | 1 | 1.725 | 2.976 |
| [1.75, 1.80) | 1.775 | 3 | 4 | 5.325 | 9.452 |
| [1.80, 1.85) | 1.825 | 4 | 8 | 7.3 | 13.323 |
| [1.85, 1.90) | 1.875 | 8 | 16 | 15 | 28.125 |
| [1.90, 1.95) | 1.925 | 5 | 21 | 9.625 | 18.53 |
| [1.95, 2.00) | 1.975 | 2 | 23 | 3.95 | 7.802 |
| 23 | 42.925 | 80.213 |
Variância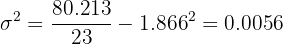
Dada a distribuição estatística, calcule a variância.
| fi | |
|---|---|
| [0, 5) | 3 |
| [5, 10) | 5 |
| [10, 15) | 7 |
| [15, 20) | 8 |
| [20, 25) | 2 |
| [25, ∞) | 6 |
| xi | fi | Fi | |
|---|---|---|---|
| [0, 5) | 2.5 | 3 | 3 |
| [5, 10) | 7.5 | 5 | 8 |
| [10, 15) | 12.5 | 7 | 15 |
| [15, 20) | 17.5 | 8 | 23 |
| [20, 25) | 22.5 | 2 | 25 |
| [25, ∞) | 6 | 31 | |
| 31 |
Média
Não podemos calcular a média, porque não é possível encontrar a marca da classe do último intervalo.
Variância
Se não há média não é possível encontrar a variância.
Considere os seguintes dados: 
. Pede-se:
a) Calcule sua média e sua variância.
b) Se todos os dados anteriores são multiplicados por 
, qual será a nova média e variância.
| xi | xi² |
|---|---|
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 6 | 36 |
| 8 | 64 |
| 10 | 100 |
| 33 | 229 |
a) Média e variância:
Média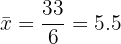
Variância
b) Se todos os valores da variável são multiplicados por um número, a média fica multiplicada por e a variância fica multiplicada pelo quadrado deste número.
Média
Variância
Gostou desse artigo? Deixe uma nota!
Loading...
