Temas
Método de substituição para sistema de equações
O método de substituição, como seu nome nos diz, consiste em isolar o valor de uma variável obtido em uma das equações e substituí-lo em outra equação.
NOTA
Quando um sistema tem mais incógnitas (variáveis) do que número de equações, então o sistema tem soluções infinitas, isto é, cada variável pode ter diferentes valores, contanto que cumpra sempre com a equação, a quantidade de valores que pode ter cada variável é infinita. Exemplo:
Dada a equação: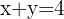 
Observe que trata-se de uma equação com duas variáveis. Rapidamente podemos nos dar conta de alguns dos valores que são solução:
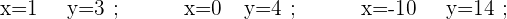
Observe que existe uma quantidade infinita de valores que podemos designar a 
e 
para que sejam solução.
Por outra parte, quando o sistema tem a mesma quantidade de equações e de incógnitas, então geralmente o sistema tem uma única solução.
Exemplo do método com sistema de 2x2
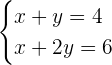
A 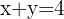chamaremos de “Equação I”
e 
é a “Equação II”
Isolamos qualquer das 2 variáveis em uma das 2 equações, (sempre devemos procurar aquela que requeira menos trabalho algébrico para nossa comodidade), neste caso, isolamos na Equação I
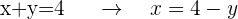
Isto chamamos de “Valor de em relação a "
Substituímos o valor isolado na outra equação, neste caso, substituímos o valor de na Equação II
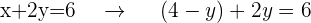
Como podemos notar, agora temos apenas a variável na equação. Esta equação pode ser simplificada e isolada para obtermos o valor de .
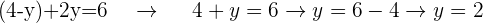
Uma vez que tenhamos o valor de uma das variáveis, neste caso o de , podemos substituí-lo em qualquer uma das 2 equações para encontrar o valor da outra variável, neste caso .
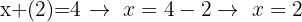
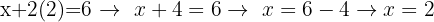
Também podemos usar a equação que havíamos isolado, que é a que mais nos convém já que nos dá diretamente o valor de x
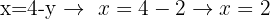
E assim obtemos o valor de nossas variáveis em um sistema de equações e podemos observar que a solução é ÚNICA.
Passos para resolver um sistema de equações lineares de 3x3
1 Escolher uma variável e isolá-la em uma das equações.
Geralmente escolhemos a variável com o menor coeficiente, e da equação mais fácil, para que possamos isolar sem tanto trabalho algébrico.
2 Substituir nas outras duas equações.
Usar o isolamento para substituir a variável em outras duas equações. As duas novas equações que são o resultado deste passo formarão um sistema de equações de 2x2.
3 Para resolver o sistema de 2x2.
Para isso repito o processo:
- Escolho uma das 2 variáveis e isolo ela em uma das equações.
- Utilizo o que foi isolado para substituir a variável na outra equação (a que não isolamos no sistema de 2x2).
- Com o passo anterior teremos uma equação linear de uma variável, que ao ser isolada, nos dará seu valor.
- O valor que obtemos vamos substituí-lo no passo de isolamento que fizemos no sistema de 2x2, dessa forma calcularemos o valor de outra variável.
4 Obtenho o valor da variável que me falta
Como no passo 3 obtemos o valor de duas das três variáveis, para encontrar a que ainda nos falta, utilizaremos o isolamento que fizemos no passo um e em seguida substituímos com as incógnitas que já resolvemos.
Exercícios de sistemas de 3 equações com 3 variáveis
Para aplicar o método de substituição, devo escolher uma equação e uma variável para isolar. Como me convém que o isolamento seja fácil, escolhemos a terceira equação, que é a que tem o coeficiente mais pequeno na variável
Este isolamento será usado para fazer uma substituição nas outras 2 equações
Assim, obtemos um novo sistema de equações de 2x2
Aqui temos que aplicar novamente o método de substituição, isto é, escolher uma equação e uma variável para isolar. A mais fácil neste caso é a primeira com a variável .
Este isolamento será usado para fazer uma substituição na outra equação
Como já sabemos que z=1, vamos utilizar o último isolamento que fizemos para encontrar y
Agora utilizamos o primeiro isolamento, o da variável que nos falta, neste caso
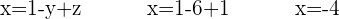
Para aplicar o método de substituição, devemos escolher uma equação e uma variável para isolar. Como nos convém que o isolamento seja fácil, escolhemos a segunda equação, que é a que tem o coeficiente mais pequeno na variável
Utilizo o que foi isolado para substituir nas outras 2 equações
Assim obtemos um novo sistema de equações de 2x2
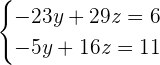
Aqui temos que aplicar novamente o método de substituição, isto é, escolher uma equação e uma variável para isolar. A mais fácil neste caso é a segunda com a variável .
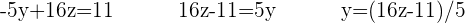
Este isolamento será usado para fazer uma substituição na outra equação. Para nos desfazermos do denominador, será necessário multiplicar toda a equação por 5
Como já sabemos que , vamos utilizar o último isolamento que fizemos para encontrar y
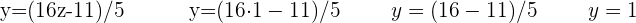
Agora pegamos o primeiro isolamento que fizemos, que é o da variável que nos falta, neste caso
Para aplicar o método de substituição, devemos escolher uma equação e uma variável para isolar. Como nos convém que o isolamento seja fácil, escolhemos a primeira equação, que é a que tem o coeficiente mais pequeno na variável
Utilizo o que foi isolado para substituir nas outras 2 equações
Assim obtemos um novo sistema de equações de 2x2
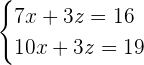
Aqui temos que aplicar novamente o método de substituição, isto é, escolher uma equação e uma variável para isolar. A mais fácil neste caso é a primeira com a variável 
.
Este isolamento será usado para fazer uma substituição na outra equação
Como já sabemos que , vamos utilizar o último isolamento que fizemos para encontrar
Agora pegamos o primeiro isolamento que fizemos, que é o da variável que nos falta, neste caso
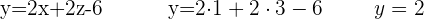
Problemas comuns resolvidos com sistemas de equações
Um cliente de um supermercado pagou um total de 
reais por 
de leite, 
de presunto serrano e 
de azeite de oliva. Calcule o preço de cada artigo, sabendo que 
de azeite custa o triplo que de leite e que 
de presunto custa o mesmo que 
de azeite mais de leite.
Declaramos as variáveis
Leite:
Presunto:
Azeite:
Cada oração nos dá uma equação que forma o seguinte sistema de equações lineares
Neste caso, duas das nossas equações já têm variáveis isoladas (Equação 2 e 3). Substituímos o valor de da segunda equação na terceira.
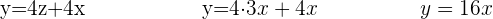
Substituímos o valor de 
e de na primeira equação
Utilizo minhas equações isoladas de e de para obter seu valor
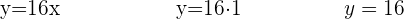
Por fim
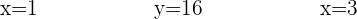
Isso quer dizer que os preços são
Leite R$ 1
Presunto R$ 16
Azeite R$ 3
Uma locadora de vídeos é especializada em filmes de três tipos:
- Infantis
- Oeste americano
- Terror
Sabemos que:
dos filmes infantis mais 
dos filmes de Oeste americano representam 
do total de filmes.
dos filmes infantis mais do filmes de Oeste americano mais dos filmes de terror representam a metade do total dos filmes.
Há 
filmes de Oeste americano à mais do que os filmes Infantis.
Encontre o número de filmes de cada tipo.
A cada elemento do exercício vamos designar uma variável.
- Infantis:
- Oeste Americano:
- Terror:
Ao escrever o problema obtenho o sistema de equações lineares de 3x3
Reescrevemos e simplificamos,
Multiplicamos toda a equação por 100 para nos desfazermos do único denominador e simplificamos a expressão obtida:
Dividimos por 
e obtemos:
Pegamos a segunda equação e seguimos os mesmos passos:
Para ter o mesmo denominador comum, multiplicamos as frações do lado direito por 
e obtemos:
Nos desfazemos do denominador e simplificamos:
Dividimos a equação por e obtemos:
Usando as versões simplificadas da primeira e a segunda equação, formamos o seguinte sistema:
Como já temos uma variável isolada em uma das equações, vamos utilizá-la para substituir o valor de nas duas equações iniciais e por fim multiplicamos a última obtida por 3.
Assim obtemos um novo sistema de equações de 2x2
Aqui temos que aplicar novamente o método de substituição, isto é, escolher uma equação e uma variável para isolar. A mais fácil neste caso é a segunda com a variável .
Este isolamento será usado para fazer uma substituição na outra equação
Como já sabemos que 
, vamos utilizar o último isolamento que fizemos para encontrar
Agora pegamos o último isolamento que fizemos, o da variável que nos falta, neste caso
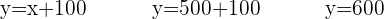
Por fim concluímos que há:
- Infantis: 500 filmes
- Oeste: 600 filmes
- Terror: 900 filmes
Os lados de um triângulo medem 
, 
e 
.
Com um centro em cada vértice, desenhamos três circunferências; e tangentes entre si de duas a duas.
Calcule as longitudes dos raios das circunferências.
Com o desenho da figura e ao usar uma variável para cada raio das 3 circunferências, sabemos o sistema
Para aplicar o método de substituição, devemos escolher uma equação e uma variável para isolar. Isolamos neste caso a variável da primeira equação
Este isolamento será usado para fazer uma substituição nas outras 2 equaçõess
Neste caso a equação não tem variável x, então deixamos como está.
Com isso tenho um novo sistema de equações de 2x2
Aqui temos que aplicar novamente o método de substituição, isto é, escolher uma equação e uma variável para isolar. A mais fácil neste caso é a segunda com a variável .
Este isolamento será usado para fazer uma substituição na outra equação
Como já sabemos que 
, vamos utilizar o último isolamento que fizemos para encontrar
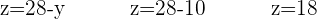
Agora pegamos o último isolamento que fizemos, o da variável que nos falta, neste caso
Gostou desse artigo? Deixe uma nota!
Loading...
Exercícios desatualizado