Temas

Exercícios com problemas de carros
Para fazer exercícios de carros que mantém velocidade constante utilizaremos as fórmulas de movimento retilíneo uniforme:
espaço = velocidade × tempo

Neste tipo de exercício podemos nos deparar com três casos:
1. Os carros vão em sentido contrário

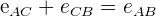
O espaço percorrido pelo primeiro até o ponto de encontro mais o espaço que o segundo percorreu é igual à distância que os separam
Exemplo:
Duas cidades  e
e  se distanciam
se distanciam 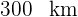 entre si. Às 9 da manhã parte da cidade
entre si. Às 9 da manhã parte da cidade  um carro em direção à cidade
um carro em direção à cidade  com uma velocidade de
com uma velocidade de  , e da cidade
, e da cidade  parte outro em direção à cidade
parte outro em direção à cidade  com uma velocidade de
com uma velocidade de  . Encontre o tempo que levarão para se encontrarem; a hora do encontro; a distância percorrida por cada um.
. Encontre o tempo que levarão para se encontrarem; a hora do encontro; a distância percorrida por cada um.
O tempo que levarão para se encontrarem
1 Conhecemos a velocidade de cada carro. Substituímos na fórmula de espaço e obtemos

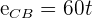
2 Sabemos que o espaço percorrido pelo primeiro carro mais o espaço percorrido pelo segundo é igual a 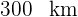
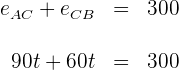
3 Resolvemos a equação anterior
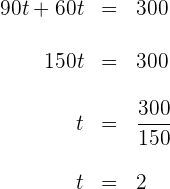
Os carros levarão 2 horas para se encontrarem.
A hora do encontro
Se encontrarão às 11 da manhã porque partem às 9 da manhã e percorrem por duas horas até se encontrarem.
A distância percorrida por cada carro
Para encontrar a distância percorrida por cada carro, substituímos o tempo 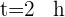 na fórmula do espaço percorrido
na fórmula do espaço percorrido
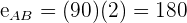
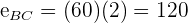
Dessa forma sabemos que o primeiro carro percorre 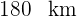 e o segundo carro percorre
e o segundo carro percorre 
2. Os carros vão no mesmo sentido

O espaço percorrido pelo primeiro carro menos o espaço percorrido pelo 2º carro é igual à distância que os separa
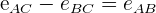
Exemplo:
Duas cidades  e
e  se distanciam
se distanciam 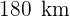 entre si. Às 9 da manhã parte um carro de cada cidade e os dois carros vão no mesmo sentido. O carro que sai de
entre si. Às 9 da manhã parte um carro de cada cidade e os dois carros vão no mesmo sentido. O carro que sai de  circula a
circula a  , e o que sai de
, e o que sai de  circula a
circula a  . Encontre o tempo que levarão para se encontrarem; a hora do encontro; a distância percorrida por cada um.
. Encontre o tempo que levarão para se encontrarem; a hora do encontro; a distância percorrida por cada um.
O tempo que levarão para se encontrarem
1 Conhecemos a velocidade de cada carro. Substituímos na fórmula de espaço e obtemos

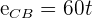
2 Sabemos que o espaço percorrido pelo primeiro carro menos o espaço percorrido pelo segundo é igual a 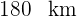
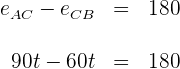
3 Resolvemos a equação anterior
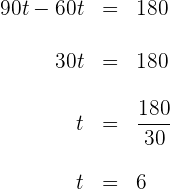
Os autos levarão 6 horas para se encontrarem.
A hora do encontro
Se encontrarão às 3 da tarde porque partem às 9 da manhã e percorrem por seis horas até se encontrarem.
A distância percorrida por cada carro
Para encontrar a distância percorrida por cada carro, substituímos o tempo 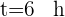 na fórmula de espaço percorrido:
na fórmula de espaço percorrido:  ,
, 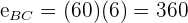 . Dessa forma sabemos que o primeiro carro percorre
. Dessa forma sabemos que o primeiro carro percorre 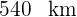 e o segundo carro percorre
e o segundo carro percorre 
3. Os carros partem do mesmo ponto e no mesmo sentido
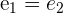
O espaço percorrido pelo primeiro carro é igual ao espaço percorrido pelo segundo.
Exemplo:
Um carro parte da cidade  com velocidade de
com velocidade de 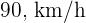 . Três horas mais tarde parte da mesma cidade outro carro no mesmo sentido a uma velocidade de
. Três horas mais tarde parte da mesma cidade outro carro no mesmo sentido a uma velocidade de 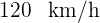 . Encontre o tempo que levará para o segundo carro alcançar o primeiro; a distância em que ocorre o encontro.
. Encontre o tempo que levará para o segundo carro alcançar o primeiro; a distância em que ocorre o encontro.
O tempo que levará para o segundo carro alcançar o primeiro.
1 Se o tempo aplicado pelo primeiro carro é  , o do segundo carro que parte três horas mais tarde será
, o do segundo carro que parte três horas mais tarde será  . Substituímos na fórmula de espaço e obtemos
. Substituímos na fórmula de espaço e obtemos
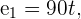

2 Sabemos que o espaço percorrido por ambos os carros é o mesmo
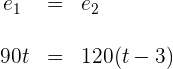
3 Resolvemos a equação anterior
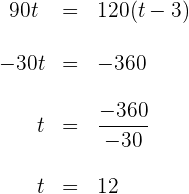
O primeiro carro leva  .
.
O segundo carro leva 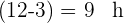 .
.
A distância em que ocorre o encontro.
Calculamos o espaço percorrido por um dos dois carros
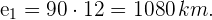
Resumir com IA:












