Equação logarítima
Em equações logarítmicas, a incógnita está no argumento do logaritmo.
Antes de resolver esse tipo de equação, é importante lembrar as propriedades dos logaritmos, pois elas serão fundamentais para fazer as expressões e encontrar a solução correta.
As propriedades dos logarítmos
1. 
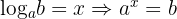
2. 
3. 
4. 
5. 
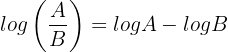
6. 
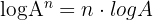
Além disso, temos que verificar os resultados para evitar o logaritmo de um número negativo ou zero, o que é comum quando há uma expressão de segundo grau no argumento do logaritmo.
Exercícios resolvidos de equações logarítmicas
Resolva as equações logarítmicas a seguir:
1. 
Para resolver esta equação, só é necessário aplicar a propriedade 
(definição de logaritmo):
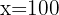
2. 
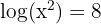
Podemos começar aplicando a propriedade 
dos logaritmos. Em seguida, isolamos a incógnita e depois aplicamos a propriedade para resolver a equação:
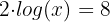
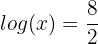
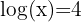
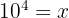
3. 
Aplicamos a propriedade 1 dos logaritmos e, em seguida, isolamos a variável 
.
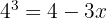
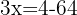
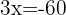
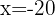
No primeiro membro, aplicamos a propriedade do logaritmo de um produto. No segundo membro, usamos a propriedade do logaritmo de uma potência.
4. 
Usando as propriedades dos logaritmos, podemos expressar cada membro da equação como um único logaritmo. Para o primeiro membro, podemos empregar a propriedade 
e, no segundo, a propriedade :
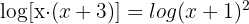
Agora que os dois membros estão escritos como um único logaritmo, podemos igualar os argumentos (propriedade de injetividade dos logaritmos):
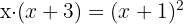
Resolvemos a equação:
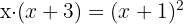
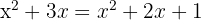
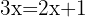
5. 
O denominador do primeiro membro multiplica o segundo membro da equação:
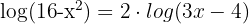
Aplicamos a propriedade e igualamos os argumentos dos algoritmos:
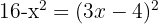
Resolvemos a equação:
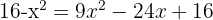
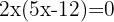
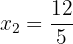
Neste caso, devemos verificar se alguma das soluções torna algum logaritmo indefinido:
Usando :
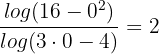
No denominador, teríamos:
o que é uma indeterminação, pois não é possível calcular o logaritmo de um número negativo. Portanto, a solução da equação é: .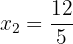
Resumir com IA:
Gostou desse artigo? Deixe uma nota!
Loading...
