
Conceito de equação do segundo grau incompleta
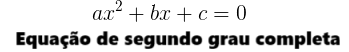
Uma equação do segundo grau é chamada de incompleta quando algum dos coeficientes b ou c, ou ambos, são iguais a zero. Assim, podemos encontrar três tipos de equações do segundo grau incompletas.
Primeiro caso
Quando ambos os coeficientes são iguais a zero, a equação do segundo grau incompleta é a seguinte:
Se b=0 e c=0 então ax² = 0 (equação do segundo grau incompleta)
Para esse tipo de equação, a solução é sempre x = 0.
Exemplos de equações do segundo grau incompletas – caso 1
1
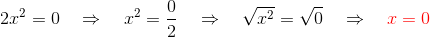
2
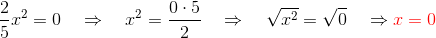
Segundo caso
Quando o coeficiente c é igual a zero, a equação do segundo grau incompleta é a seguinte:
Se c=0 entãos ax² + bx = 0 (equação de segundo grau incompleta).
Vamos ver como as soluções são encontradas:
Colocamos o fator comum x em evidência.
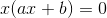
Como temos um produto igualado a zero, igualamos os fatores a zero.
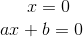
Portanto, os resultados são:
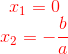
Exemplos de equações do segundo grau incompletas – caso 2
1 
Colocamos o fator comum x em evidência.
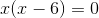
Como temos um produto igualado a zero, igualamos os fatores a zero.
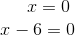
As soluções são:

2 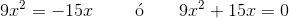
Colocamos o fator comum 3x em evidência.
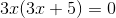
Como temos um produto igualado a zero, igualamos os fatores a zero.
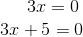
Os resultados são:
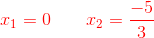
Terceiro caso
Quando o coeficiente b é igual a zero, a equação do segundo grau incompleta é a seguinte:
Se b=0 então ax² + c = 0 (equação do segundo grau incompleta).
Vamos ver como encontrar as soluções:
Passamos o termo c para o segundo membro, trocando o sinal.
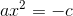
Passamos o coeficiente a para o segundo membro, dividindo.
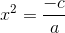
Efetuamos a raiz quadrada em ambos os lados da igualdade e obtemos duas soluções, uma positiva e outra negativa, ou seja:
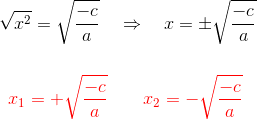
Exemplos de equações do segundo grau incompletas – caso 3
1 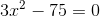
Passamos o termo c para o segundo membro, trocando o sinal.
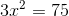
Passamos o coeficiente a para o segundo membro, dividindo.
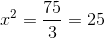
Efetuamos a raiz quadrada em ambos os lados da igualdade e obtemos duas soluções, uma positiva e outra negativa, ou seja:
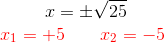
2 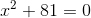
Passamos o termo c para o segundo membro, trocando o sinal.
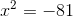
Passamos o coeficiente a para o segundo membro dividindo, mas como ele é igual a 1, o resultado é o mesmo que no passo anterior.
Ao efetuar a raiz quadrada em ambos os lados da igualdade, obtemos um radicando negativo, que não possui solução no conjunto dos números reais.
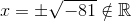
Resumir com IA:












