Temas

Como encontramos a equação da reta conhecendo dois pontos?
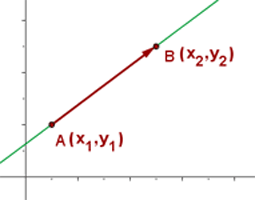
Sejam os pontos 
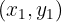 e
e 
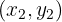 que determinam uma reta
que determinam uma reta  .
.
Um vetor diretor da reta é:
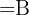
Cujos componentes são:
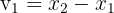 e
e 
Substituindo estes valores na fórmula contínua:
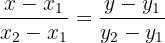
Podemos encontrar a equação da reta.
Encontre a equação da reta conhecendo dois pontos
Encontre a equação da reta que passa por
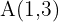 e
e 
Substituímos os valores na fórmula contínua:

Então, a equação da reta é:
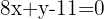
Conhecendo a equação da reta, encontre 2 pontos nela
Quando conhecemos a equação de uma reta é muito fácil encontrar os pontos que pertencem à ela. Devemos recordar que a equação da reta pode ser escrita de várias formas: geral, paramétrica ou declive, por exemplo.
Para encontrar pontos na reta, o mais recomendado é usar a fórmula do declive e fazer uma tabulação (tabela de valores), onde encontramos muitas coordenadas (pontos) que pertencem à reta
Exemplo:
Seja a equação geral da reta: 
Podemos escrevê-la na sua forma declive (isolando y): 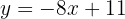
Agora podemos atribuir qualquer valor para  , e obter o valor correspondente para y.
, e obter o valor correspondente para y.
Outra forma fácil de obtermos  pontos da reta de forma rápida é lembrando-se o que significa cada elemento da equação com declive:
pontos da reta de forma rápida é lembrando-se o que significa cada elemento da equação com declive:
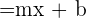
Onde  representa o declive da reta e
representa o declive da reta e  representa a coordenada do ponto onde a reta atravessa o eixo
representa a coordenada do ponto onde a reta atravessa o eixo  , ou seja, saber isso nos dirá rapidamente que um ponto na reta é a coordenada:
, ou seja, saber isso nos dirá rapidamente que um ponto na reta é a coordenada:
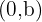 .
.
Agora, supomos em nossa equação a variável  . Então temos
. Então temos 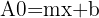 . Isolamos
. Isolamos  :
:
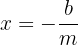
Este valor é conhecido como  e é o valor onde a reta atravessa o eixo
e é o valor onde a reta atravessa o eixo  . Saber isso nos dirá rapidamente que um ponto na reta é a coordenada
. Saber isso nos dirá rapidamente que um ponto na reta é a coordenada 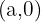
De tal forma que, na equação que usamos de exemplo, obteríamos os pontos 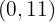 e
e 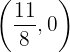
Resumir com IA:












