Temas
A elipse é uma curva geométrica fascinante que aparece em diversos aspectos da natureza e das ciências. Desde a antiguidade, matemáticos e astrónomos vêm estudando e admirando a beleza e as propriedades únicas dessa figura.
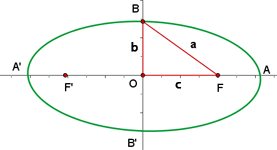
Em sua forma mais básica, uma elipse é o conjunto de todos os pontos em um plano para os quais a soma das distâncias até dois pontos fixos, chamados de focos, é constante.
Equação reduzida da elipse com eixo horizontal
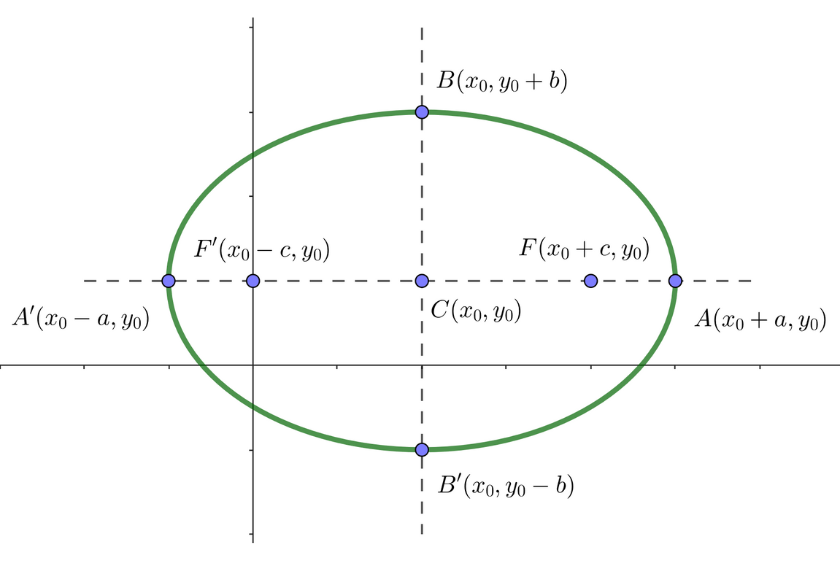
Consideramos o centro da elipse coincidindo com a origem do sistema de coordenadas e os eixos da elipse alinhados com os eixos coordenados. As coordenadas dos focos são:
y 
. Además cualquier punto 
sobre la elipse cumple que
.
Podemos observar que a expressão é equivalente a:
.
Desenvolvendo e resolvendo essa última expressão, temos o equivalente a:
.
onde 
, como podemos observar na imagem anterior.
Determine os elementos característicos e a equação reduzida da elipse de focos: 
e 
, e de eixo maior com medida de 
.
Temos esse gráfico do problema:
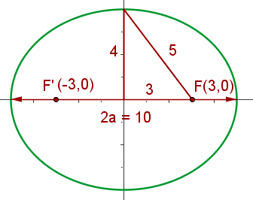
Note que o centro da elipse é o ponto médio entre os focos, ou seja,
portanto, o centro está na origem. Observe também que os focos estão localizados sobre o eixo 
, logo, o eixo maior também está. Sabemos que 
representa a metade do comprimento do eixo maior, portanto 
, sendo o semieixo maior.
Sabemos ainda que a metade da distância focal 
corresponde à distância de qualquer um dos focos até o centro da elipse, e temos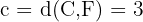 
.
Por fim, podemos determinar o semieixo menor a partir do semieixo maior e de , sabendo que o semieixo menor obedece à relação , ou seja,
de onde obtemos 
. Com isso, a equação reduzida da elipse é:
.
Equação de eixo horizontal da elipse
Se o centro da elipse 
e o eixo principal é paralelo ao eixo das abscissas (eixo 
), os focos tem as coordenadas 
e 
. E a equação canônica de la elipse será:
onde e 
são semieixos maior e menos, respectivamente. Uma vez removidos os denominadores e feito o desenvolvimento desarrollar, obtém-se, normalmente, uma equação do tipo:
Onde 
e 
têm o mesmo sinal. Essa última fórmula é conhecida como equação geral da elipse.
Determine a equação canônica da elipse de foco 
, de vértice 
e de centro 
Primeiramente, observamos que o eixo maior é paralelo ao eixo xxx (eixo das abscissas). Podemos perceber isso analisando o centro e um dos focos — o foco está simplesmente deslocado para a direita em relação ao centro da elipse. Com isso, podemos escrever a equação da elipse no formato:
Agora, sabemos que representa o semieixo maior. Ele corresponde à distância entre o centro da elipse e o vértice, logo:
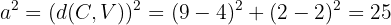
Além disso, o semieixo menor satisfaz a relação , em que é a distância entre o centro da elipse e o foco. Assim:
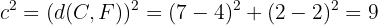
Portanto:
Isso nos leva à equação:
Determinar o centro, os semieixos, os vértices e os focos da elipse de equação:
Como a equação já está na forma reduzida, identificamos que o centro é 
.
Para encontrar os semieixos, observamos que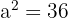 
, portanto 
, e também que 
,
logo .
Como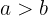 
, é o semieixo maior e é o semieixo menor.
Note que aparece no denominador da expressão 
, o que indica que o eixo maior da elipse é paralelo ao eixo .
Isso significa que os vértices estão a unidades à direita e a unidades à esquerda do centro.
Assim, os vértices são 
e 
.
Por fim, vamos determinar os focos.
Sabemos que a metade da distância focal (isto é, a distância do centro da elipse até um dos focos) é representada por , e ela satisfaz a relação 
.
Assim, temos:
Logo, 
, e os focos são 
e 
.
Equação reduzida de eixo vertical da elipse
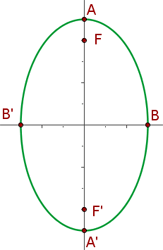
Se o eixo principal está sobre eixo das ordenadas, você terá a seguinte equação:
Onde as coordenadas dos focos são 
e 
Determine as coordenadas dos vértices, focos e a excentricidade da elipse com equação reduzida.
Primero, vamos encontrar a metade da distância focal. Sabemos que a metade da distância focal é e satisfaz 
, assim:
,
Assim: 
.
Agora que já temos esse valor, os focos passam a ter coordenadas:
y 
.
Para encontrar os vértices, vamos relembrar que eles estão em: unidades acima e abaixo do centro da elipse, portanto, dado que
, os vértices são:
e 
.
Por fim, temos que a excentricidade da elipse é igual a:
.
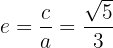Equação de eixo vertical da elipse
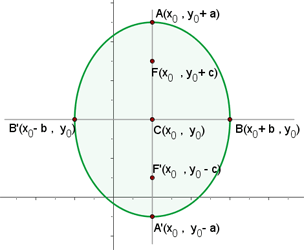
De maneira geral, se o centro da elipse é (pode ser na origem ou não) e o eixo é paralelo ao eixo das ordenadas (
), então os focos tem coordenadas 
e 
e a equação da elipse será:
Exercícios
Considerando as equacões gerais das elipses, escreve de forma reduzida, obtenha as coordenadas dos focos, vértices, calcule as excentricidades e represente no gráfico.
a. 
Para obter a equação em sua forma reduzida, é necessário apenas fazer uso de álgebra básica:
Observemos que a última igualdade já está na forma reduzida da equação da elipse. A partir dessa equação, fica claro que o centro da elipse é 
.
Além disso, pela equação, identificamos que o semieixo maior é 
e o semieixo menor é 
.
Como o semieixo maior está associado ao termo com , isso indica que o eixo maior da elipse é paralelo ao eixo das abscissas.
Assim, os vértices estão localizados a unidades à esquerda e à direita do centro, com coordenadas 
e 
.
Para encontrar os focos, precisamos calcular a metade da distância focal, representada por , que satisfaz a relação . Portanto, temos:
Essa igualdade nos mostra que 
.
Sendo assim, os focos estão a unidades de distância à esquerda e à direita do centro da elipse, com coordenadas
e 
.
Por fim, a excentricidade da elipse é dada por
A seguir, temos o gráfico da elipse:
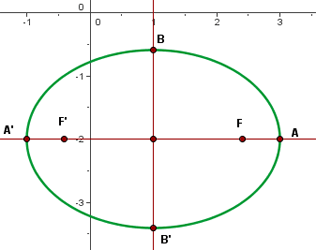
b. 
Para obter a equação em sua forma reduzida, é necessário apenas fazer uso de álgebra básica:
Observamos que a última igualdade já representa a equação da elipse na sua forma reduzida.
A partir dessa equação, é evidente que o centro da elipse é 
.
Além disso, pela equação, identificamos que o semieixo maior é 
e o semieixo menor é 
.
Como o semieixo maior está associado ao termo com 
, concluímos que o eixo maior da elipse é paralelo ao eixo das ordenadas.
Sendo assim, os vértices estão localizados a unidades acima e abaixo do centro da elipse, com coordenadas 
e 
.
Para encontrar os focos, precisamos calcular a metade da distância focal, representada por , que satisfaz a relação . Portanto:
Essa igualdade nos diz que 
.
Assim, os focos estão a unidades de distância acima e abaixo do centro da elipse, com coordenadas:
e 
.
Por fim, a excentricidade da elipse é dada por:
A seguir, temos o gráfico da elipse:
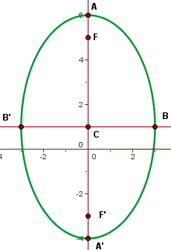
c. 
Novamente fazemos uso da álgebra básica para obter a equação reeduzida.
Observamos que a última igualdade já representa a equação da elipse na sua forma reduzida.
A partir dessa equação, fica claro que o centro da elipse é 
.
Além disso, pela equação, identificamos que o semieixo maior é 
e o semieixo menor é 
.
Como o semieixo maior está associado ao termo com , concluímos que o eixo principal da elipse é paralelo ao eixo das abscissas.
Sendo assim, os vértices estão localizados a unidades à direita e à esquerda do centro da elipse, com coordenadas 
e 
.
Para encontrar os focos, precisamos calcular a metade da distância focal, representada por , que satisfaz a relação .
Assim, temos:
Essa igualdade nos dá 
.
Logo, os focos estão a unidades de distância à esquerda e à direita do centro da elipse, com coordenadas 
e 
.
Por fim, a excentricidade da elipse é dada por:
A seguir, temos o gráfico da elipse:
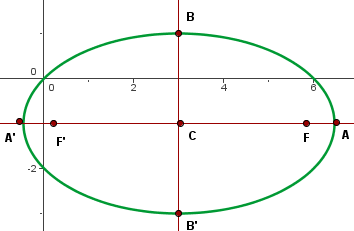
d. 
Novamente fazemos uso da álgebra básica para obter a equação reeduzida.
Observamos que a última igualdade já representa a equação da elipse na sua forma reduzida.
A partir dessa equação, é evidente que o centro da elipse é 
.
Além disso, identificamos que o semieixo maior é 
e o semieixo menor é 
.
Como o semieixo maior está associado ao termo com , concluímos que o eixo principal da elipse é paralelo ao eixo das ordenadas.
Assim, os vértices estão a unidades acima e abaixo do centro da elipse, com coordenadas 
e 
.
Para determinar os focos, precisamos calcular a metade da distância focal, indicada por , que satisfaz a equação .
Portanto, temos:
Essa igualdade nos leva a 
.
Os focos, então, estão localizados a unidades acima e abaixo do centro da elipse, com coordenadas 
e 
.
Por fim, a excentricidade da elipse é dada por:
A seguir, temos o gráfico da elipse:
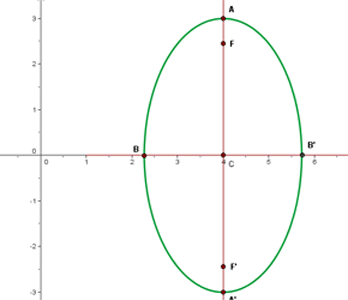
Encontre a equação da elipse conhecendo os seguintes dados:
a. 
Para resolver este exercício, primeiro notemos que podemos obter facilmente , que é a distância entre o foco e o centro (distância focal), portanto 
.
Também notemos que é simples obter o semieixo maior, já que este é a distância entre o vértice e o centro, portanto .
Por fim, temos que o semieixo menor podemos determinar a partir do semieixo maior e da distância focal, já que satisfaz:
, portanto:
Isto nos diz que 
.
Por fim, lembremos que se os focos estão à direita e à esquerda do centro da elipse, então:
o quadrado do semieixo maior divide o termo que envolve .
Por outro lado, se os focos estão acima ou abaixo do centro, então o quadrado do semieixo maior divide o termo que envolve .
Dito isso, nossa equação é:
b.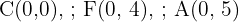 
Neste exercício, a distância entre o foco e o centro é e a distância entre o vértice e o centro é .
Utilizando novamente a relação entre os eixos e a distância focal, temos:
Portanto, .
Como os focos estão acima e abaixo do centro da elipse, o quadrado do semieixo maior divide o termo com .
Assim, a equação reduzida é:
c.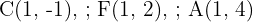 
Para resolver este exercício, primeiro notemos que podemos obter facilmente , que é a distância entre o foco e o centro (a metade da distância focal).
Portanto 
.
Também notemos que é simples obter o semieixo maior, já que este é a distância entre o vértice e o centro, portanto
.
Por fim, temos que o semieixo menor podemos determinar a partir do semieixo maior e da distância focal, já que satisfaz
, portanto,
Isto nos diz que .
Por fim, lembremos que se os focos estão à direita e à esquerda do centro da elipse, então:
o quadrado do semieixo maior divide o termo que envolve .
Por outro lado, se os focos estão acima ou abaixo do centro, então o quadrado do semieixo maior divide o termo que envolve .
Dito isso, nossa equação é:
d.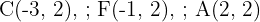 
Para resolver este exercício, primeiro notemos que podemos obter facilmente , que é a distância entre o foco e o centro (meia distância focal), portanto:
.
Também notemos que é simples obter o semieixo maior, já que este é a distância entre o vértice e o centro, portanto:
.
Por fim, temos que o semieixo menor podemos determinar a partir do semieixo maior e da distância focal, já que satisfaz:
, portanto:
Isto nos diz que 
.
Por fim, lembremos que se os focos estão à direita e à esquerda do centro da elipse, então:
o quadrado do semieixo maior divide o termo que envolve .
Por outro lado, se os focos estão acima ou abaixo do centro, então o quadrado do semieixo maior divide o termo que envolve .
Dito isso, nossa equação é:
Escreva a equação reduzida da elipse cujo centro é a origem, que passa pelo ponto 
e cujo eixo menor (paralelo ao eixo das ordenadas) mede 
.
O fato de que o eixo menor mede nos diz diretamente que .
Agora, notemos que a elipse passa pelo ponto , isso implica que para 
e 
satisfaz a equação da elipse, assim:
já substituindo esse ponto e o valor de , unicamente precisamos isolar da equação e encontrar seu valor.
Que nos dá a equação:
Sabemos que uma elipse tem seu centro na origem, a metade de sua distância focal é . Um ponto da elipse dista de seus focos 
e 
, respectivamente. Calcule a equação reduzida dessa elipse se seu eixo maior está sobre o eixo das ordenadas.
O fato de que a metade de sua distância focal seja nos diz diretamente que 
, ou seja,
. Agora, sabemos que a soma das distâncias dos focos a um ponto é sempre 
, isso implica que:
Já que temos e , podemos obter :
Dado que o eixo maior da elipse está sobre o eixo das ordenadas, temos que a equação está dada por:
Determine a equação reduzida de uma elipse cuja distância focal é 
e a área do retângulo construído sobre os eixos é 
. Consideremos o eixo maior da elipse paralelo ao eixo das abscissas.
Vamos analisar os dados que temos.
Primeiro, sabemos que a distância focal é , o que implica que 
e, portanto, 
.
Também sabemos que a área do retângulo que contém a elipse é 
. Essa área é igual ao eixo maior vezes o eixo menor da elipse, já que essas são as medidas dos lados do retângulo.
Além disso, o eixo maior da elipse mede , enquanto o eixo menor mede 
. Isso indica que latex(2b) = 4ab = 80[/latex].
Agora, observamos que podemos isolar uma variável em função da outra; neste caso, vamos isolar 
.
Também sabemos da relação 
, mas já temos o valor de e que .
Substituindo esses valores na primeira igualdade, poderemos obter o valor de .
As raízes do polinômio que encontramos são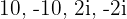 
.
Observamos que, como deve ser real e estritamente positivo, a única solução que satisfaz isso é 
.
Substituímos esse valor na igualdade para encontrar que .
Já que temos os valores dos semieixos, procedemos à escrita da equação.
Como a elipse tem eixo maior sobre o eixo das abscissas, temos que o termo dividido pelo quadrado do semieixo maior é o que possui as , ou seja:
Determine a equação reduzida de uma elipse sabendo que um dos vértices dista 
de um foco e 
do outro. Suponhamos que a elipse tenha centro na origem e eixo maior sobre o eixo das abscissas, por simplicidade.
A imagem a seguir nos ajudará a entender as distâncias mencionadas e como, a partir delas, calcular e , para finalmente poder calcular .
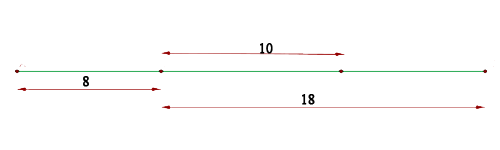
A distância do vértice ao foco mais distante é , enquanto a distância ao mais próximo é .
Observemos que, se subtrairmos a distância ao foco mais próximo da distância ao mais distante, obteremos a distância focal.
Assim, teríamos que 
, ou seja, 
.
Por outro lado, notemos que se somarmos a distância do vértice ao foco mais distante com a distância ao mais próximo, obteremos a distância de um vértice ao outro.
Portanto, teríamos que 
, ou seja, 
.
Uma vez que temos esses valores, podemos calcular o quadrado do semieixo menor, já que:
.
Assim, nossa equação será:
.
Encontre a equação reduzida de uma elipse sabendo que ela passa pelo ponto 
e sua excentricidade é 
. Suponhamos que a elipse tenha centro na origem e eixo maior sobre o eixo das abscissas.
Primeiro, temos que a excentricidade é 
, isolando temos:
.
Por outro lado, dado que ela passa pelo ponto , temos que esse ponto satisfaz a equação da elipse, ou seja:
Observemos que já temos o valor de e .
Além disso, sabemos que .
Substituímos esses valores de e e obtemos .
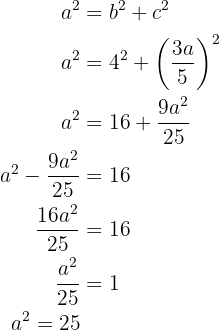
Agora, vamos escrever a equação:
Escreva a equação da elipse cujo centro é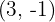 
, que passa pelo ponto 
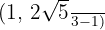e cujo eixo maior (paralelo ao eixo das abscissas) mede .
Como o centro não está na origem e o eixo maior é paralelo ao eixo das abscissas, a equação é da forma:
O fato de o eixo maior medir nos diz diretamente que .
Agora, notemos que a elipse passa pelo ponto 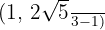, isso implica que para:
e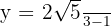 
se satisfaz a equação da elipse.
Assim, já substituindo esse ponto e o valor de , precisamos apenas isolar na equação e encontrar seu valor:
O que nos dá a equação:
Determine a equação da elipse com centro em , distância focal de 
, eixo menor paralelo ao eixo das abscissas e de comprimento .
Como o centro não está na origem e o eixo menor é paralelo ao eixo das abscissas, a equação é da forma:
Analisemos os dados que temos.
Primeiro, temos que a distância focal é 
, isso implica que:
e, portanto, 
.
Também temos que o comprimento do eixo menor é , o que implica que:
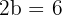e, portanto, .
Sabemos também da relação , mas já temos os valores de e .
Substituindo esses valores na igualdade poderemos obter o valor de .
E podemos escrever a equação:
Encontre a equação da elipse com centro em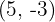 
, sabendo que sua excentricidade é 
, seu eixo maior mede e é paralelo ao eixo das abscissas.
Como o centro não está na origem e o eixo maior é paralelo ao eixo das abscissas, a equação é da forma:
Temos que o eixo maior mede , isso implica que:
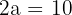e, portanto, .
Sabemos que a excentricidade é:
.
Isolando, temos 
.
Note que já temos os valores de e .
Sabemos que .
Substituindo esses valores, podemos encontrar :
E assim, escrevemos a equação:
Gostou desse artigo? Deixe uma nota!
Loading...
