Definição de circunferência
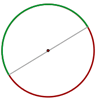
Uma circunferência é uma linha curva fechada cujos pontos estão todos à mesma distância de um ponto fixo chamado centro, como mostrado na figura a seguir.
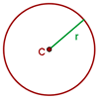
Elementos da circunferência
Centro da circunferência
Ponto do qual todos os pontos da circunferência estão à mesma distância.
Raio da circunferência
Segmento que liga o centro da circunferência a um ponto qualquer dela.
Corda
Segmento que une dois pontos da circunferência.
Diâmetro
Corda que passa pelo centro da circunferência.
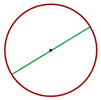
Arco
Um arco de circunferência é cada uma das partes em que uma corda divide a circunferência.
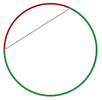
Semicircunferência
Cada um dos arcos iguais determinados por um diâmetro.
É dada pela fórmula: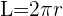 
Comprimento de um arco de circunferência
Costuma-se associar a cada corda o menor arco por ela delimitado.
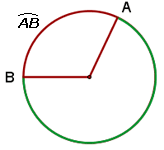
Um arco de circunferência é representado pelo símbolo
sobre as letras dos pontos extremos do arco.
As letras são escritas no sentido anti-horário, isto é, no sentido contrário ao dos ponteiros do relógio.
Comprimento de um arco de circunferência
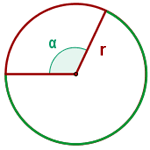
É dada pela fórmula: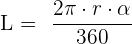 
Exercícios de circunferência
O comprimento de uma circunferência é: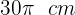 
. Encontre o raio.
Aplicamos a fórmula do comprimento da circunferência:
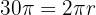
Isolando o raio, obtemos:
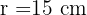
Calcule o comprimento de uma roda com 
cm de diâmetro.
A circunferência que temos é a seguinte:
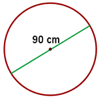
Para aplicar a fórmula, precisamos conhecer o raio, ou seja:
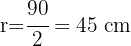
Agora, aplicando a fórmula do comprimento da circunferência:
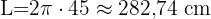
Calcule a área do quadrado inscrito em uma circunferência de comprimento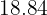 
cm.
Dada a figura a seguir:
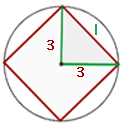
e substituindo os dados na fórmula do comprimento da circunferência, temos:
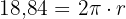
Isolando o raio, obtemos:
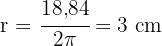
Aplicando o Teorema de Pitágoras, calculamos a medida do lado do quadrado:
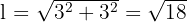
Portanto, a área do quadrado inscrito na circunferência é:
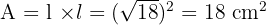
Os braços de um balanço medem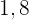 
m de comprimento e podem descrever, no máximo, um ângulo de 
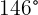. Calcule o espaço percorrido pelo assento do balanço quando o ângulo descrito no seu movimento é máximo.
Substituímos os valores diretamente na fórmula:
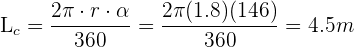
Um farol varre com sua luz um ângulo plano de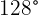 
. Se o alcance máximo do farol é de 
milhas, qual é o comprimento máximo, em metros, do arco correspondente?
Considerando que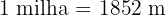 
e substituindo na fórmula:
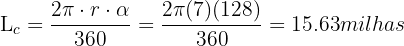
Por último, convertemos as milhas em metros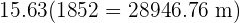 
Ângulos na circunferência
Ângulo central
O ângulo central tem seu vértice no centro da circunferência e seus lados são dois raios.
A medida de um arco é igual à medida de seu ângulo central correspondente.
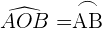
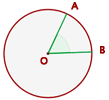
Ângulo inscrito
O ângulo inscrito tem seu vértice na circunferência e seus lados são secantes a ela.
Mede a metade do arco que abrange.
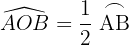
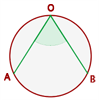
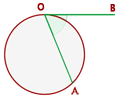
Ângulo semi-inscrito
O vértice do ângulo semi-inscrito está na circunferência; um de seus lados é secante e o outro é tangente a ela.
Mede a metade do arco que abrange.
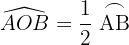
Ângulo interior
Seu vértice está no interior da circunferência e seus lados são secantes a ela.
Mede a metade da soma das medidas dos arcos correspondentes aos seus lados e às prolongações de seus lados.
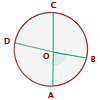
Ángulo exterior
Seu vértice é um ponto exterior à circunferência, e os lados do ângulo podem ser: ambos secantes, um tangente e outro secante, ou ambos tangentes à circunferência.
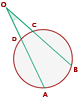
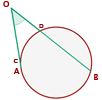
Mede a metade da diferença entre as medidas dos arcos correspondentes aos seus lados sobre a circunferência.
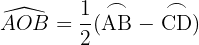
Resumir com IA:
Gostou desse artigo? Deixe uma nota!
Loading...
