Temas

O que é a racionalização de radicais?
A racionalização de radicais consiste em eliminar os radicais do denominador, o que facilita o cálculo de operações como a soma de frações.
Podemos distinguir três casos principais:
Caso 1
Racionalização do tipo 
Multiplica-se o numerador e o denominador por 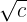 .
.
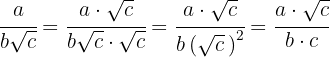
Exemplos
1 Racionalizar a expressão 
Multiplicamos numerador e denominador pela raiz de 2, realizamos os cálculos e simplificamos a fração:

2 Racionalizar a expressão 
Para realizar a soma, racionalizamos o segundo somando multiplicando e dividindo pela raiz de 2 e realizamos a soma:


Caso 2
Racionalização do tipo 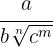
Multiplica-se o numerador e o denominador por 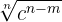 .
.

Exemplo
Racionalizar a expressão: 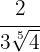
O radicando  pode ser escrito em sua forma de potência:
pode ser escrito em sua forma de potência: 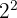
Então, devemos multiplicar o numerador e denominador pela raiz quinta de 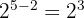
Multiplicamos os radicais do denominador, extraímos fatores do radical e simplificamos a fração:

Caso 3
Racionalização do tipo 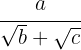
De modo geral, quando o denominador for um binômio com pelo menos um radical,
Multiplica-se o numerador e o denominador pelo conjugado do denominador.
O conjugado de um binômio é o binômio com o sinal central trocado:

Além disso, devemos lembrar que a soma por diferença é igual à diferença de quadrados:
(a+b)(a−b)=a2−b2(a+b)(a-b) = a^2 - b^2

Exemplos
1 Racionalizar a expressão 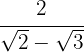
Multiplicamos o numerador e o denominador pelo conjugado do denominador, eliminamos os parênteses no numerador e realizamos a soma por diferença no denominador, o que resulta em uma diferença de quadrados:
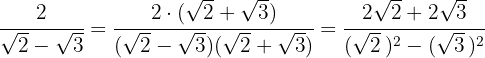
Do denominador extraímos os radicandos e dividimos por  , ou seja,mudamos o sinal do numerador.
, ou seja,mudamos o sinal do numerador.
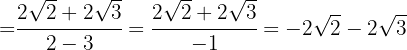
2 Racionalizar a expressão 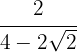
Multiplicamos e dividimos a fração pelo conjugado do denominador

Fazemos a soma por diferença no denominador e simplificamos: 
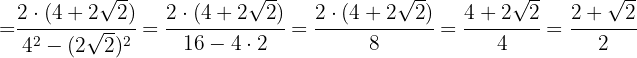
3 Racionalizar a expressão 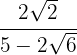
Multiplicamos o numerador e o denominador pelo conjugado do denominador, eliminamos os parênteses no numerador e realizamos a soma por diferença no denominador, o que resulta em uma diferença de quadrados.
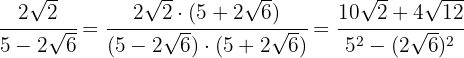
No numerador, vamos decompor o  em fatores para serem extraídos e terminamos realizando as operações do denominador
em fatores para serem extraídos e terminamos realizando as operações do denominador

Exemplos de exercícios de racionalização de radicais
1 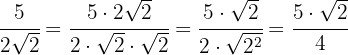
2 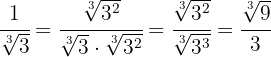
3 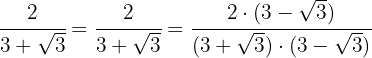
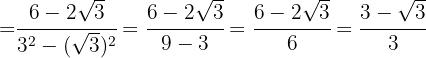
4 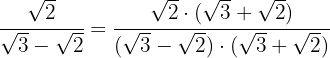

5 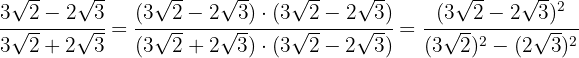
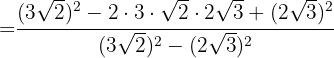
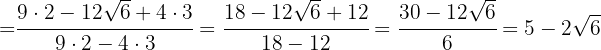
Resumir com IA:












