Temas
O cálculo da distância entre dois pontos é uma ferramenta essencial em diversos campos, desde a geometria até a navegação e a ciência de dados. Ele permite medir a separação entre dois locais em um espaço, seja em um plano bidimensional ou em um espaço tridimensional. Esse conceito de distância não é apenas fundamental na matemática, mas também possui aplicações práticas no dia a dia, como calcular a distância entre cidades em um mapa, determinar a proximidade entre objetos em um espaço tridimensional ou até mesmo avaliar semelhanças entre conjuntos de dados.
Seja explorando o mundo das coordenadas cartesianas no plano ou avançando para dimensões superiores, o cálculo da distância entre dois pontos oferece uma base sólida para entender relações espaciais e aplicar esses conhecimentos em diversas disciplinas. Vamos começar a medir distâncias e descobrir a importância desse conceito essencial!
Distância entre dois pontos
Para estudar a distância entre dois pontos, observe a seguinte figura:
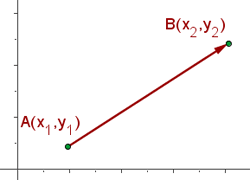
No gráfico conseguimos apontar dois pontos 
e 
no plano cartesiano unidos por um vetor. A magnitude do vetor, destacado em vermelho, que liga esses pontos, representa o valor da distância entre os pontos e .
Fórmula para calcular a distância entre dois pontos e o teorema de Pitágoras
A fórmula para calcular essa magnitude é dada pela seguinte expressão:
Esse valor pode ser obtido usando o Teorema de Pitágoras. Para isso, considere o triângulo retângulo cujos vértices são os pontos:
, e 
.
Podemos notar que o valor da hipotenusa desse triângulo é a distância entre os pontos:
e .
Uma vez que a magnitude dos segmentos que unem e , e são 
e 
respectivamente.
O Teorema de Pitágoras afirma que o valor da hipotenusa ou a distância entre e é 
Exemplos de distância entre dois pontos
1 Calcule a distância entre os pontos: 
e 
2 Determine a condição para que os pontos 
e 
estejam a uma unidade de distância.
Se a distância entre 
e 
é um, isso quer dizer que:
elevando ao quadrado para eliminar a raiz:
3 Demonstre que os pontos: 
, 
e 
pertencem a uma circunferência com centro 
.
Se 
é centro da circunferencia, para que 
e 
sejam parte de uma circunferência, por definição as distâncias de a , a e a devem ser iguais. Vamos demonstrar, utilizando a fórmula da distância entre dois pontos.
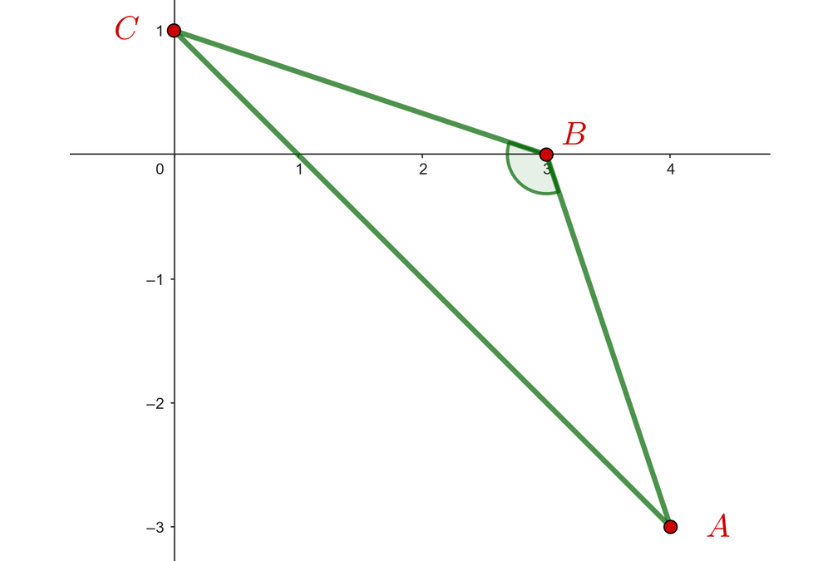
4 Classifique o triângulo determinado pelos pontos: 
, 
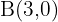e 
Primeiro, vamos calcular as distâncias entre os pontos do triângulo para poder classificar seu tipo.
Já que 
, podemos concluir que não se trata de um triângulo equilátero, pois, se fosse, as distâncias entre quaisquer de seus pontos seriam iguais.
Além disso, se:
trata-se de um triângulo acutângulo,
quando 
é um triângulo retângulo,
e finalmente, se 
será um triângulo obtusângulo.
Dessa forma,
Portanto, a figura trata-se de um triângulo obtusângulo.
Gostou desse artigo? Deixe uma nota!
Loading...
