Exercícios e problemas resolvidos de programação linear - otimização

Uma companhia fabrica e vende dois modelos de lâmpada L1 e L2. Para sua fabricação é necessário um trabalho manual de 20 minutos para o modelo L1 e de 30 minutos para o L2; e um trabalho com uso de máquina de 20 minutos para o modelo L1 e de 10 minutos para L2.
A fábrica dispõe de 100 horas ao mês para o trabalho manual e 80 horas ao mês para o trabalho com máquina. Sabendo que o lucro por unidade é de 15 e 10 reais para L1 e L2, respectivamente. Planifique a produção para obter o máximo de lucro.

Escolha das incógnitas

x = nº de lâmpadas L1

y = nº de lâmpadas L2

Função objetivo

f(x, y) = 15x + 10y

Restrições

Convertemos os minutos em horas

20 min = 1/3 h

30 min = 1/2 h

10 min = 1/6 h

Para escrever as restrições vamos utilizar uma tabela:

                       L1     L2      Tempo
Manual       1/3     1/2    100
Máquina    1/3     1/6      80

1/3x + 1/2y ≤ 100

1/3x + 1/6y ≤ 80

Como o número de lâmpadas são números naturais, teremos mais duas restrições:

x ≥ 0

y ≥ 0

Encontre o conjunto de soluções factíveis

Temos que representar graficamente as restrições.
Ao ser x ≥ 0 e y ≥ 0, trabalharemos no primeiro quadrante.
Representaremos as retas a partir de seus pontos de interseção com os eixos.

Resolvemos graficamente a inequação: 1/3 x + 1/2 y ≤ 100; Para isso, pegamos um ponto do plano, por exemplo, (0,0).

1/3·0 + 1/2·0 ≤ 100

1/3·0 + 1/6·0 ≤ 80

A zona de interseção dos resultados das inequações seria a solução para o sistema de inequações, que por sua vez, constitui o conjunto das soluções factíveis.

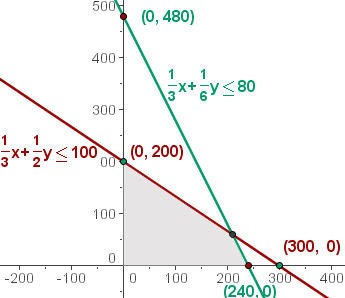
Calcule as coordenadas dos vértices da área da solução factível

A solução ótima, se única, encontra-se no vértice do perímetro. Estas são as soluções para os sistemas:

1/3x + 1/2y = 100; x = 0                                    (0, 200)

1/3x + 1/6y = 80; y = 0                                      (240, 0) 

1/3x + 1/2y = 100; 1/3x + 1/6y = 80              (210, 60) 

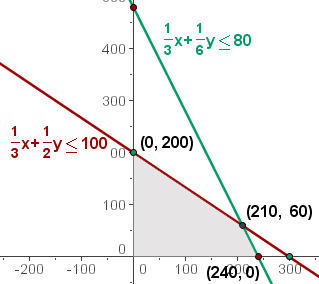
Calcule o valor da função objetivo

Na função objetivo substituímos cada um dos vértices.

f(x, y) = 15x + 10y

f(0, 200) = 15·0 + 10·200 = R$ 2.000

f(240, 0 ) = 15·240 + 10·0 = R$ 3.600

f(210, 60) = 15·210 + 10·60 = R$ 3.750 Máximo

A solução ótima do problema é fabricar 210 do modelo L1 e 60 do modelo L1 para obtermos um lucro de R$ 3750,00.
 

Com o início do ano escolar são lançadas ofertas para a compra de material.
Algumas lojas querem oferecer 600 cadernos, 500 fichários e 400 canetas, com oferta, embalando-os em dois conjuntos da seguinte forma:

• O primeiro conjunto com 2 cadernos, 1 fichário e 2 canetas.
• O segundo conjunto com 3 cadernos, 1 fichário e 1 caneta.
• Os preços de cada conjunto serão de 6.5 e 7 R$, respectivamente.

Quantos conjuntos de cada tipo seriam necessários para se obter o máximo de lucro?
 Escolha das incógnitas.

x = P1

y = P2

Função objetivo

f(x, y) = 6.5x + 7y

Restrições

          P1      P2 Disponíveis
Cadernos 2  3                       600
Fichários 1   1                        500
   Canetas 2  1                        400

2x + 3y ≤ 600

x + y ≤ 500

2x + y ≤ 400

x ≥ 0

y ≥ 0

Encontre o conjunto de soluções factíveis

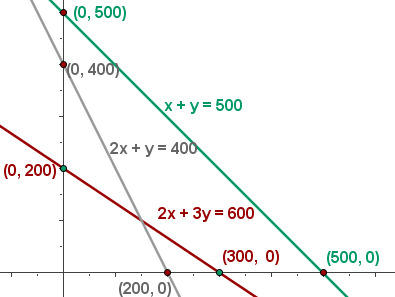
Calcule as coordenadas dos vértices da área da solução factível.

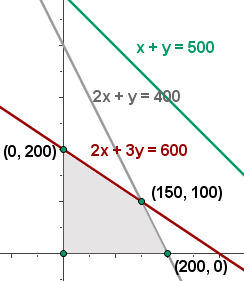
Calcule o valor da função objetivo

f(x,y) = 6.5 · 200 + 7 · 0 = R$ 1 300

f(x,y)= 6.5 · 0 + 7 · 200 = R$ 1 400

f(x,y)= 6.5 · 150 + 7 · 100 = R$ 1 675 Máximo

A solução ótima são 150 P1 e 100 P2 com a qual obtemos R$1675,00 

Em uma granja é aplicada uma dieta para engordar galinhas em cuja ração encontra-se uma composição mínima de 15 unidades de uma substância A e 15 unidades de outra substância B.

No mercado é possível encontrar apenas duas classes de composto alimentar: o tipo X com uma composição de uma unidade de A e 5 de B, e outro tipo Y, com uma composição de cinco unidades de A e uma de B. O preço do tipo X é de 10 reais e do tipo Y de 30 reais.

Qual a quantidade que deve-se comprar de cada tipo de composto para cobrir as necessidades com um custo mínimo?

Escolha das incógnitas

x = X

y = Y

Função objetivo

f(x,y) = 10x + 30y

Restrições

     X   Y   Mínimo
A   1    5    15
B   5    1    15

x + 5y ≥ 15

5x + y ≥ 15

x ≥ 0

y ≥ 0

Encontre o conjunto de soluções factíveis

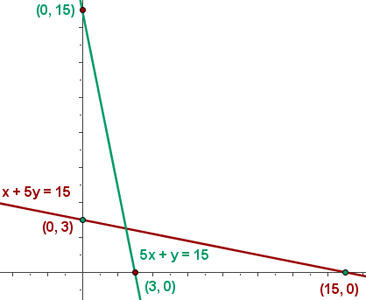
Calcule as coordenadas dos vértices da área da solução factível.

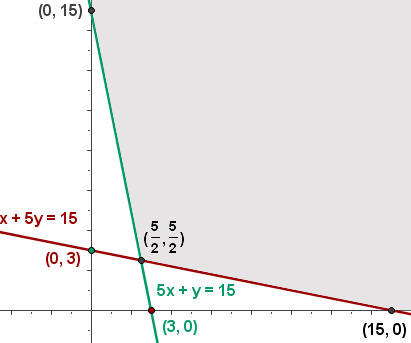
Calcule o valor da função objetivo

f(0, 15) = 10 · 0 + 30 · 15 = 450

f(15, 0) = 10 · 15 + 30 · 0 = 150

f(5/2, 5/2) = 10 · 5/2 + 30 · 5/2 = 100   Mínimo

O custo mínimo é R$ 100 para X = 5/2 e Y = 5/2.

São utilizados 600 g de um determinado fármaco para elaborar comprimidos grandes e pequenos. Os grandes pesam 40 g e os pequenos 30 g.
São necessários ao menos três comprimidos grandes e ao menos o dobro de comprimidos pequenos. Cada comprimido grande proporciona um lucro de R$2  e o pequeno de R$1.

Quantos comprimidos de cada tipo deve-se produzir para obtermos o lucro máximo?

Escolha das incógnitas.

x = Número de comprimidos grandes

y = Número de comprimidos pequenos

Função objetivo

f(x, y) = 2x + y

Restrições

40x + 30y ≤ 600

x ≥ 3

y ≥ 2x

x ≥ 0

y ≥ 0

Encontre o conjunto de soluções factíveis

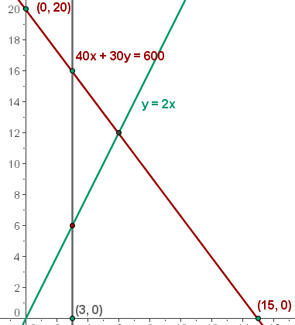
Calcule as coordenadas dos vértices da área da solução factível.

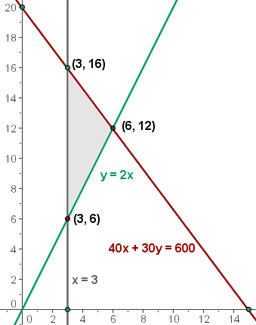
Calcule o valor da função objetivo

f(x, y) = 2 · 3 + 16 = R$ 22

f(x, y) = 2 · 3 + 6 = R$ 12

f(x, y) = 2 · 6 + 12 = R$ 24 Máximo

O máximo de lucro é de R$ 24, fabricando 6 comprimidos grandes e 12 pequenos.

Algumas grandes lojas querem liquidar 200 camisas e 100 calças da última temporada. Para isso lançam duas ofertas, A e B.
A oferta A consiste em um conjunto de camisa e calça a R$ 30; a oferta B consiste em um conjunto de três camisas e uma calça a R$ 50. Não se espera vender menos de 20 conjuntos da oferta A e nem menos de 10 da oferta B.

Quantos conjuntos de cada tipo devem ser vendidos para se obter o máximo de lucro?

Escolha das incógnitas.

x = nº de conjuntos de A

y = nº de conjuntos de B

Função objetivo

f(x, y) = 30x + 50y

Restrições

                     A   B   Mínimo
Camisas     1    3   200
Calças         1     1   100

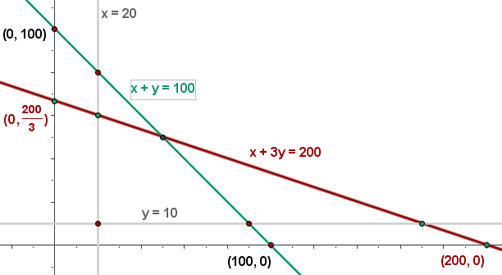
x + 3y ≤ 200

x + y ≤ 100

x ≥ 20

 y ≥ 10

Encontre o conjunto de soluções factíveis

Calcule as coordenadas dos vértices da área da solução factível.

Calcule o valor da função objetivo

f(x, y) = 30 · 20 + 50 · 10 = R$ 1100

f(x, y) = 30 · 90 + 50 · 10 = R$ 3200

f(x, y) = 30 · 20 + 50 · 60 = R$ 3600

f(x, y) = 30 · 50 + 50 · 50 = R$ 4000 Máximo

Com 50 conjuntos de cada tipo obtemos um lucro máximo de R$ 4000.