Uma equação de primeiro grau (também conhecida como equação linear, já que é elaborado um gráfico da equação, onde é obtido uma linha reta) é uma igualdade de duas expressões algébricas, onde estão presentes uma ou mais incógnitas (todas elas com expoente  ), cujos valores podem ser relacionados através de operações aritméticas. De seguida, propomos alguns exercícios sobre equações de primeiro grau. Vamos lá?
), cujos valores podem ser relacionados através de operações aritméticas. De seguida, propomos alguns exercícios sobre equações de primeiro grau. Vamos lá?

 Isolamos a incógnita, dividindo os dois membros por
Isolamos a incógnita, dividindo os dois membros por  . Também, de maneira prática, podemos dizer que
. Também, de maneira prática, podemos dizer que  que está multiplicando o primeiro membro, passa a dividir o segundo.
que está multiplicando o primeiro membro, passa a dividir o segundo.


 Agrupamos os termos semelhantes, temos que somar os dois membros
Agrupamos os termos semelhantes, temos que somar os dois membros  e
e  , de modo que obtemos uma equação equivalente.
, de modo que obtemos uma equação equivalente.
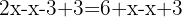
Na prática, é comum dizer que se um termo está somando  em um membro, passa ao outro membro subtraindo
em um membro, passa ao outro membro subtraindo  e se estava subtraindo
e se estava subtraindo  passa para o outro membro somando
passa para o outro membro somando  . Somamos:
. Somamos:



latex]2(2x-3)=6+x[/latex]Utilizamos a propriedade distributiva para operar o parêntesis, isto é, multiplicar por  cada termo algébrico que está dentro do parêntesis, assim, do lado esquerdo temos:
cada termo algébrico que está dentro do parêntesis, assim, do lado esquerdo temos: 
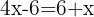
Agrupamos os termos semelhantes, o x que está somando, passa ao outro membro subtraindo e o  que está subtraindo, passa somando. Somamos:
que está subtraindo, passa somando. Somamos:

Isolamos a incógnita, o  que está multiplicando passa ao outro membro dividindo
que está multiplicando passa ao outro membro dividindo


 Para poder tirar os denominadores, é necessário encontrar o mínimo múltiplo comum de
Para poder tirar os denominadores, é necessário encontrar o mínimo múltiplo comum de  e
e 

Multiplicamos ambos os membros da equação por el m.c.m, neste caso  , e obtemos:
, e obtemos:
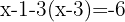
Multiplicamos usando a propriedade distributiva para resolver o parêntesis, agrupamos e somamos os termos semelhantes:
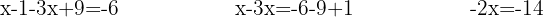
Isolamos a incógnita:
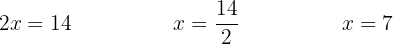

 Multiplicamos
Multiplicamos  por cada termo dentro do parêntesis (propriedade distributiva) para resolver o parêntesis e simplificamos:
por cada termo dentro do parêntesis (propriedade distributiva) para resolver o parêntesis e simplificamos:

Agrupamos e somamos os termos semelhantes:


 Usando a propriedade distributiva para calcular os parêntesis, multiplicamos o primeiro parêntesis por
Usando a propriedade distributiva para calcular os parêntesis, multiplicamos o primeiro parêntesis por  e o segundo por
e o segundo por  .
.
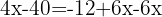
Agrupamos os termos semelhantes
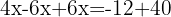
Somamos os termos semelhantes e isolamos


 Usando a propriedade distributiva para resolver os parêntesis, multiplicamos o primeiro parêntesis por
Usando a propriedade distributiva para resolver os parêntesis, multiplicamos o primeiro parêntesis por  e o segundo por
e o segundo por  .
.

Agrupamos os termos semelhantes
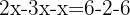
Somamos os termos semelhantes e isolamos


 Para poder tirar os denominadores, é necessário encontrar o mínimo múltiplo comum de
Para poder tirar os denominadores, é necessário encontrar o mínimo múltiplo comum de  ;
;  e
e 
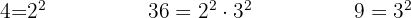
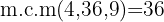
Dividimos o denominador comum entre cada denominador e multiplicamos o resultado pelo numerador correspondente
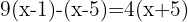
Usando a propriedade distributiva para calcular os parêntesis, multiplicamos o primeiro parêntesis por  , o segundo por
, o segundo por  e o terceiro por
e o terceiro por  .
.
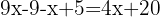
Agrupamos os termos semelhantes

Somamos os termos semelhantes e isolamos

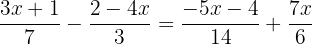
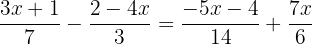 Para poder tirar os denominadores, é necessário encontrar o mínimo múltiplo comum de
Para poder tirar os denominadores, é necessário encontrar o mínimo múltiplo comum de  ,
, ,
, e
e  .
.


Dividimos o denominador comum entre cada denominador e multiplicamos o resultado pelo numerador correspondente

Usando a propriedade distributiva para calcular os parêntesis, multiplicamos o primeiro parêntesis por  o segundo por
o segundo por 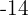 , e o terceiro por
, e o terceiro por  .
.
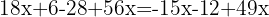
Agrupamos os termos semelhantes

Somamos os termos semelhantes e isolamos

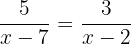
latex]\displaystyle \frac{5}{x-7}=\frac{3}{x-2}[/latex]Para que se cumpra a igualdade entre as duas frações, é necessário que o produto dos extremos seja igual ao produtos dos meios.
Ou se preferir, também é possível encontrar o m.c.m. que é  porque os dois binômios são irredutíveis. Em seguida dividimos o m.c.m. por cada denominador e multiplicamos o resultado pelo numerador correspondente.
porque os dois binômios são irredutíveis. Em seguida dividimos o m.c.m. por cada denominador e multiplicamos o resultado pelo numerador correspondente.
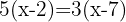
Usando a propriedade distributiva para calcular os parêntesis, multiplicamos o primeiro parêntesis por  e o segundo por
e o segundo por  .
.
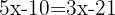
Somamos os termos semelhantes
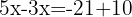
Isolamos a incógnita:

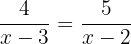
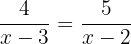 Para que se cumpra a igualdade entre as duas frações, é necessário que o produto dos extremos seja igual ao produtos dos meios.
Para que se cumpra a igualdade entre as duas frações, é necessário que o produto dos extremos seja igual ao produtos dos meios.
Ou se preferir, também é possível encontrar o m.c.m. que é 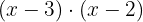 porque os dois binômios são irredutíveis. Em seguida dividimos o m.c.m. por cada denominador e multiplicamos o resultado pelo numerador correspondente.
porque os dois binômios são irredutíveis. Em seguida dividimos o m.c.m. por cada denominador e multiplicamos o resultado pelo numerador correspondente.
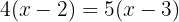
Usando a propriedade distributiva para calcular os parêntesis, multiplicamos o primeiro parêntesis por  e o segundo por
e o segundo por  .
.
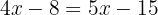
Agrupamos os termos semelhantes

Isolamos a incógnita:
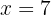
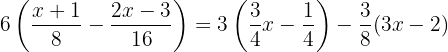
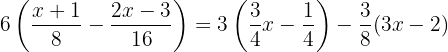 Usando a propriedade distributiva para calcular os parêntesis, multiplicamos o primeiro parêntesis por
Usando a propriedade distributiva para calcular os parêntesis, multiplicamos o primeiro parêntesis por  , e o segundo por
, e o segundo por  e o terceiro por
e o terceiro por  .
.
É preciso lembrar que quando multiplicamos um número inteiro por uma fração, resolvemos multiplicando o inteiro pelo numerador da fração e o denominador fica igual.
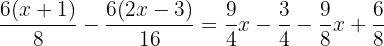
Aplicamos a propriedade distributiva para calcular os parêntesis nos numeradores
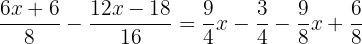
Para poder tirar os denominadores, é necessário encontrar o mínimo múltiplo comum de  ,
,  e
e  .
.
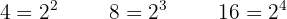

Dividimos o denominador comum entre cada denominador e multiplicamos o resultado pelo numerador correspondente.
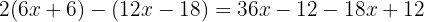
Usando a propriedade distributiva para calcular os parêntesis, multiplicamos o primeiro parêntesis por  e simplificamos com cuidado as mudanças de sinais.
e simplificamos com cuidado as mudanças de sinais.

Agrupamos os termos semelhantes
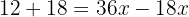
Isolamos a incógnita:
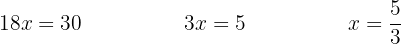
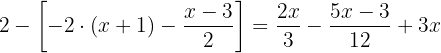
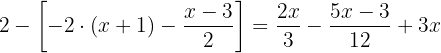 Neste caso é conveniente calcular primeiro a operação
Neste caso é conveniente calcular primeiro a operação 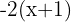 . Ao resolvê-la, podemos trocar o colchete por um parêntesis.
. Ao resolvê-la, podemos trocar o colchete por um parêntesis.

Calculamos os termos dentro do parêntesis por −1 para poder tirar o sinal negativo e o parênteses da equação:
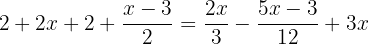
Para poder tirar os denominadores, é necessário encontrar o mínimo múltiplo comum de 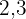 e
e  .
.
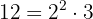
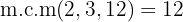
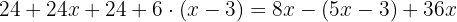
Usando a propriedade distributiva para calcular os parêntesis, multiplicamos o primeiro parêntesis por  e o segundo por
e o segundo por  :
:
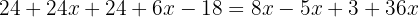
Agrupamos os termos semelhantes:
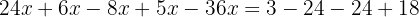
Somamos:

Dividimos os dois membros por: 

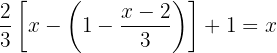
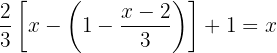 Calculamos os termos dentro do parêntesis por
Calculamos os termos dentro do parêntesis por  para poder tirar o sinal negativo e o parênteses da equação, agora podemos substituir o colchete por um parênteses.
para poder tirar o sinal negativo e o parênteses da equação, agora podemos substituir o colchete por um parênteses.
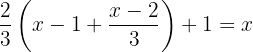
Usamos a propriedade distributiva para calcular os parênteses.
É necessário recordar que quando multiplicamos uma fração por outra, deve-se multiplicar o numerador pelo numerador e o denominador pelo denominador.
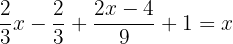
Para poder tirar os denominadores, é necessário encontrar o mínimo múltiplo comum de  e
e  .
.



Agrupamos os termos semelhantes:

Somamos e isolamos:

Resumir com IA:


