
Enunciado do Teorema de Pitágoras
O Teorema de Pitágoras estabelece o seguinte:
Para todo triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.
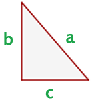
A partir desse enunciado, obtemos a seguinte fórmula, com a qual podemos calcular a medida de qualquer um dos lados de um triângulo retângulo:
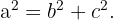
Aplicações do Teorema de Pitágoras
Calculando a hipotenusa
1 Conhecendo os dois catetos, podemos calcular a hipotenusa. Basta isolar a variável  da equação:
da equação:
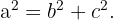
Fazemos isso simplesmente extraindo a raiz quadrada:
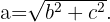
Exemplo: Os catetos de um triângulo retângulo medem  e
e  respectivamente. Qual é a medida da hipotenusa?
respectivamente. Qual é a medida da hipotenusa?
Neste caso, temos que 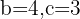 e precisamos encontrar o valor de
e precisamos encontrar o valor de 
Substituindo na fórmula anterior:
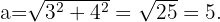
Portanto, a hipotenusa mede 
Calculando um cateto
2 Conhecendo a hipotenusa e um dos catetos, podemos calcular o outro cateto.
A partir da equação inicial 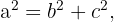 podemos isolar o valor de um dos catetos. Para o cateto
podemos isolar o valor de um dos catetos. Para o cateto 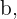 obtemos:
obtemos:
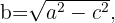
e para o cateto 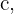

Exemplo: A hipotenusa de um triângulo retângulo mede 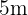 e um de seus catetos
e um de seus catetos  Qual é a medida do outro cateto?
Qual é a medida do outro cateto?
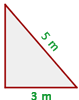
De acordo com a figura, temos que o cateto  mede
mede  , a hipotenusa
, a hipotenusa  e precisamos encontrar o cateto
e precisamos encontrar o cateto  . Dessa forma, vamos utilizar a fórmula para calcular catetos,
. Dessa forma, vamos utilizar a fórmula para calcular catetos,

Portanto cateto  mede
mede 
Classificação de triângulos retângulos
3. Conhecendo os lados de um triângulo, podemos confirmar se é ou não um triângulo retângulo.
Para que um triângulo seja retângulo, o quadrado do maior lado deve ser igual à soma dos quadrados dos dois lados menores.
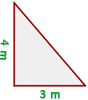
Exemplo: Determine se o triângulo a seguir é retângulo.
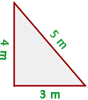
Observamos que o maior lado deste triângulo tem comprimento  Seguindo a indicação anterior, devemos verificar as seguintes igualdades:
Seguindo a indicação anterior, devemos verificar as seguintes igualdades:
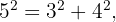
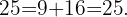
Como obtemos o mesmo resultado em ambos os lados da igualdade, podemos concluir que o triângulo é retângulo.
Exercícios
Um triângulo retângulo isósceles tem hipotenusa de 10 m de comprimento. Qual é o comprimento de seus catetos?
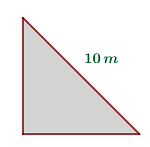
Como o triângulo é retângulo e isósceles, então seus dois catetos são iguais. Aplicamos o Teorema de Pitágoras ao triângulo com hipotenusa  e lado
e lado  :
:
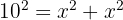
Resolvendo, vamos obter:

Assim, os catetos medem 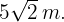
Uma escada de 10 m de comprimento está apoiada em uma parede. A base da escada está a 6 m da parede. Qual é a altura alcançada pela escada na parede?
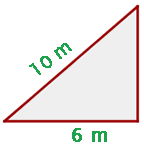
A escada, a parede e o chão formam um triângulo retângulo, no qual podemos tomar como hipotenusa o comprimento da escada, e como um dos catetos a distância da base da escada até a parede. Então, temos  e
e 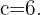
Nosso objetivo é calcular a altura que a escada alcança na parede, ou seja, encontrar o outro cateto. De acordo com as fórmulas anteriores e com a figura:

Calcule a área de um triângulo equilátero:
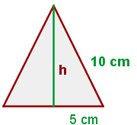
Primeiro, traçamos a altura do triângulo equilátero. Essa altura divide o triângulo em dois triângulos retângulos, com catetos  a altura do triângulo equilátero,
a altura do triângulo equilátero,  metade da base de um dos lados do triângulo e hipotenusa
metade da base de um dos lados do triângulo e hipotenusa  , o lado do triângulo inicial. Para encontrar a altura, aplicamos a fórmula para cateto em triângulo retângulo:
, o lado do triângulo inicial. Para encontrar a altura, aplicamos a fórmula para cateto em triângulo retângulo:


Sabemos que a área de um triângulo é dada pela fórmula:
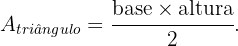
Neste caso, a base do triângulo é 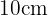 e a altura é
e a altura é 
Substituindo na fórmula da área, temos:
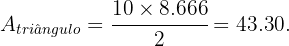
Encontre a diagonal de um quadrado:
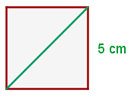
A diagonal de um quadrado com lados medindo 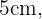 divide a figura em dois triângulos retângulos, em que a diagonal
divide a figura em dois triângulos retângulos, em que a diagonal  coincide com a hipotenusa em qualquer um dos triângulos. Precisamos, portanto, calcular a hipotenusa de um triângulo retângulo com catetos iguais a
coincide com a hipotenusa em qualquer um dos triângulos. Precisamos, portanto, calcular a hipotenusa de um triângulo retângulo com catetos iguais a 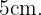
Utilizando a fórmula da hipotenusa:


Sendo assim, a diagonal mede 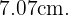
Calcule a diagonal de um retângulo:
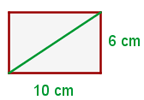
De forma semelhante ao exercício anterior, a diagonal  do retângulo divide a figura em dois triângulos retângulos, com catetos de
do retângulo divide a figura em dois triângulos retângulos, com catetos de 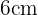 e
e 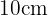 e a diagonal corresponde à hipotenusa.
e a diagonal corresponde à hipotenusa.
Vamos utilizar novamente a fórmula para a hipotenusa:
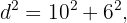
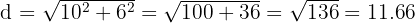
Assim, a diagonal tem comprimento de 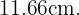
Calcule o perímetro e a área do trapézio retângulo:
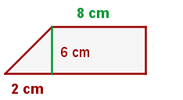
O perímetro do trapézio é a soma do comprimento de seus lados. Pela figura, sabemos que o lado superior do trapézio mede  o lado inferior mede
o lado inferior mede 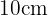 e a altura do trapézio mede
e a altura do trapézio mede 
Para calcular o lado diagonal do trapézio, que chamaremos de 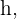 devemos considerar o triângulo retângulo formado por um lado vertical de
devemos considerar o triângulo retângulo formado por um lado vertical de  lado horizontal
lado horizontal 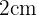 e hipotenusa
e hipotenusa 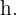 Como precisamos encontrar o valor de
Como precisamos encontrar o valor de 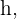 usaremos a fórmula para o cálculo da hipotenusa. Assim, temos:
usaremos a fórmula para o cálculo da hipotenusa. Assim, temos:
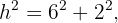
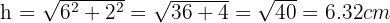
Agora podemos calcular o perímetro, que é:
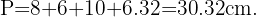
Para obter a área, observamos que o trapézio é formado por um triângulo retângulo e um retângulo. Então, sua área será a soma das áreas do triângulo e do retângulo. Ou seja:
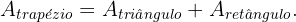
A área do retângulo é simplesmente o produto da base pela altura, então: 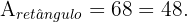
A área do triângulo é dada por:
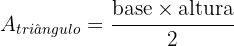
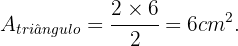
Portanto:
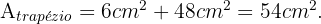
O perímetro de um trapézio isósceles é 110 m, e suas bases medem 40 m e 30 m, respectivamente. Calcule os lados não paralelos e a área.
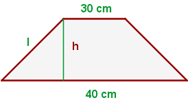
O perímetro do trapézio é igual à soma dos comprimentos de todos os lados. Assim, temos a seguinte igualdade 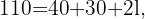 onde
onde  é o comprimento de cada um dos lados não paralelos. Isolando
é o comprimento de cada um dos lados não paralelos. Isolando  da equação anterior, temos que:
da equação anterior, temos que:
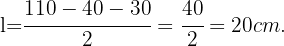
Dessa forma, resolvemos a primeira parte do problema.
Agora, lembrando que a área do trapézio é igual à soma das bases multiplicada pela altura, dividida por dois, precisamos calcular a altura do trapézio, que chamaremos de 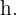
Pela figura, podemos considerar o triângulo retângulo de catetos 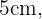
 e com hipotenusa
e com hipotenusa 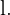 Para encontrar o valor de
Para encontrar o valor de  , vamos usar a fórmula para calcular catetos:
, vamos usar a fórmula para calcular catetos:
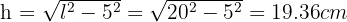
Agora podemos calcular a área do trapézio:
Encontre a área de um pentágono regular:
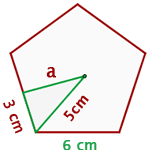
Sabemos que os lados do pentágono regular medem  Como a área do pentágono é igual à metade do produto do perímetro pelo apótema, precisamos encontrar o valor do apótema, que chamaremos de
Como a área do pentágono é igual à metade do produto do perímetro pelo apótema, precisamos encontrar o valor do apótema, que chamaremos de 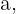 conforme a figura.
conforme a figura.
Para calcular 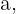 consideramos o triângulo com catetos
consideramos o triângulo com catetos 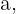
 e hipotenusa
e hipotenusa 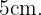 Utilizando a fórmula para catetos:
Utilizando a fórmula para catetos:
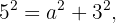
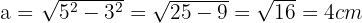
O perímetro do pentágono é:
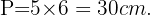
Assim, a área do pentágono será:
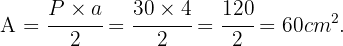
Calcule a área de um quadrado inscrito em uma circunferência de comprimento 18,84 m.
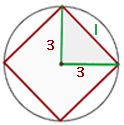
Como o quadrado está inscrito em uma circunferência, ele pode ser dividido em  triângulos retângulos com catetos iguais ao raio da circunferência,
triângulos retângulos com catetos iguais ao raio da circunferência,  , e hiputenusa igual ao lado do quadrado
, e hiputenusa igual ao lado do quadrado  . Assim, podemos usar a fórmula da hipotenusa para calcular o lado o triângulo:
. Assim, podemos usar a fórmula da hipotenusa para calcular o lado o triângulo:
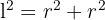
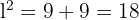 .
.
Portanto, como a área do quadrado é 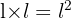 , então:
, então:
Em uma circunferência, uma corda mede 48 cm e está a 7 cm do centro. Calcule a área do círculo.
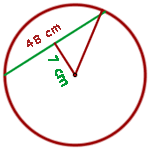
Para calcular a área do círculo, primeiro precisamos encontrar o raio. Como a corda está a  do centro, podemos formar um triângulo retângulo com catetos
do centro, podemos formar um triângulo retângulo com catetos  , metade da corda,
, metade da corda,  e e hipotenusa igual ao raio do círculo,
e e hipotenusa igual ao raio do círculo,  . Desta forma, para encontrar o raio, vamos utilizar a fórmula da hipotenusa:
. Desta forma, para encontrar o raio, vamos utilizar a fórmula da hipotenusa:
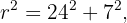
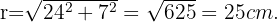
A área do círculo é dada por:
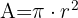

Resumir com IA:












