A circunferência e sua equação
A circunferência pode ser definida como o lugar geométrico dos pontos do plano que estão equidistantes de um ponto fixo  que chamamos centro.
que chamamos centro.
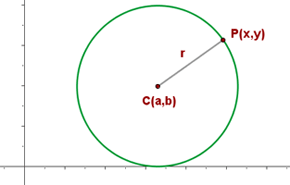
Portanto, cada ponto  da circunferência satisfaz:
da circunferência satisfaz:

onde a distância  é chamada de raio. Assim, temos a seguinte equação:
é chamada de raio. Assim, temos a seguinte equação:

Elevando ao quadrado a equação acima, obtemos:

Essa equação é conhecida como a equação reduzida da circunferência. Para obter a equação geral, desenvolvemos os quadrados dos binômios:

Em seguida, reagrupamos os termos da seguinte forma:

Consideramos as seguintes substituições:

Portanto, a equação da circunferência pode ser escrita da seguinte maneira:

Essa é chamada de equação geral da circunferência. Aqui, o centro é dado por:

e o raio satisfaz a relação:

É importante observar que a equação

deve satisfazer as seguintes condições para representar uma circunferência:
- A desigualdade abaixo deve ser satisfeita:

- A equação não pode conter o termo
 (ou seja,
(ou seja,  e
e  não podem estar multiplicados entre si).
não podem estar multiplicados entre si). - Os coeficientes de
 e
e  devem ser iguais a 1.
devem ser iguais a 1.
Observação: caso os coeficientes de  e
e  sejam diferentes de 1, ambos devem ser iguais entre si. Nesse caso, podemos dividir a equação por esse coeficiente comum para obter a equação geral da circunferência.
sejam diferentes de 1, ambos devem ser iguais entre si. Nesse caso, podemos dividir a equação por esse coeficiente comum para obter a equação geral da circunferência.
Observação: se o centro da circunferência coincide com a origem do sistema de coordenadas, então a equação da circunferência (seja na forma reduzida ou geral) é simplificada para:

Essa forma é chamada de equação canônica da circunferência.
Exercícios de equação reduzida da circunferência
Escreva a equação da circunferência com centro em  e raio 2.
e raio 2.
A equação reduzida da circunferência é:

Para obter a equação geral, desenvolvemos os binômios ao quadrado:

Agrupando os termos semelhantes:

Dada a circunferência cuja equação é  , encontre seu centro e seu raio.
, encontre seu centro e seu raio.
O centro é dado por:
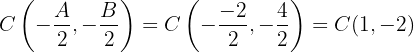
O raio é obtido por:
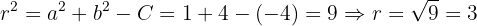
Encontre a equação da circunferência que passa pelos pontos  ,
,  e
e  .
.
Para isso, usamos a equação geral da circunferência:

Substituindo os pontos:
Com  :
:
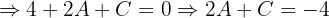
Com  :
:
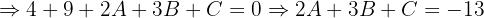
Com  :
:
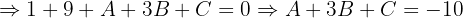
Temos o sistema:

Resolvendo o sistema, obtemos:
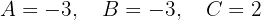
Portanto, a equação geral da circunferência é:
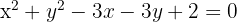
A equação  representa uma circunferência? Se sim, determine o centro e o raio.
representa uma circunferência? Se sim, determine o centro e o raio.
Os coeficientes de  e
e  são iguais, então dividimos por 4:
são iguais, então dividimos por 4:
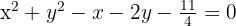
Não há termo  , e a condição de existência do raio é satisfeita.
, e a condição de existência do raio é satisfeita.
Por último, vamos verificar que satisfaça a desiguadade com os termos  e
e  .
.
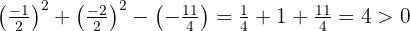
Como cumpre a três condições, então a equação pode ser considerada uma circunferência.
Para encontrar o centro, temos:

Logo, o raio satisfaz:

 .
.
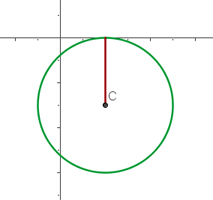
Calcule a equação da circunferência com centro em  e tangente ao eixo das abscissas.
e tangente ao eixo das abscissas.
Pede-se que seja encontrado uma circunferência tangente a uma reta.
Sempre que isso ocorre, o raio será igual à distância entre o centro da circunferência e a reta à qual ela deve ser tangente. Portanto, precisamos calcular essa distância.
Primeiro, lembramos que o eixo das abscissas é a reta  . Além disso, a distância entre um ponto
. Além disso, a distância entre um ponto  e a reta
e a reta  é:
é:

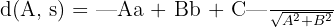
Assim, a distância entre o ponto  e a reta
e a reta  é:
é:
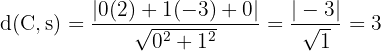
Portanto, a equação reduzida da circunferência é:

A representação gráfica dessa circunferência pode ser vista na figura a seguir.
Calcule a equação da circunferência com centro em  e tangente ao eixo das ordenadas.
e tangente ao eixo das ordenadas.
Calcule a equação da circunferência com centro em  e que é tangente ao eixo das ordenadas.
e que é tangente ao eixo das ordenadas.
Assim como no exercício anterior, devemos encontrar a distância entre o centro e o eixo das ordenadas.
Lembrando que o eixo das ordenadas é dado pela equação 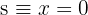 . Dessa forma, a distância é:
. Dessa forma, a distância é:
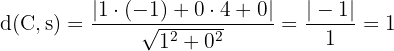
Portanto, a equação da circunferência é:
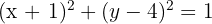
A representação gráfica da circunferência pode ser vista na figura a seguir:
Calcule a equação da circunferência com centro na interseção das retas 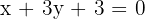 e
e  , e raio 5.
, e raio 5.
Para encontrar a equação da circunferência, basta encontrar a interseção entre as duas retas (o raio já é conhecido). Para isso, igualamos as equações:
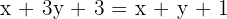
Daí obtemos  , ou seja,
, ou seja,  .
.
Substituindo em qualquer das equações, encontramos  .
.
Portanto, o centro é  e a equação da circunferência é:
e a equação da circunferência é:
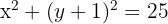
ou, na forma geral:
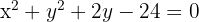
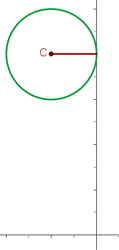
A representação gráfica pode ser vista na figura a seguir.
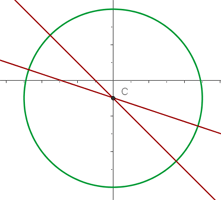
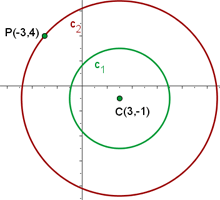
Encontre a equação da circunferência que passa por  e é concêntrica à circunferência
e é concêntrica à circunferência 
Este problema pode ser resolvido de duas maneiras diferentes:
A mais simples é perceber que todas as circunferências concêntricas a
 terão uma equação da forma:
terão uma equação da forma:
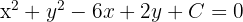
Portanto, devemos substituir o ponto  para encontrar o valor de
para encontrar o valor de  , o que nos dá:
, o que nos dá:
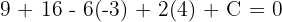
Ou seja,  , portanto,
, portanto,
 . Assim, a equação da circunferência é:
. Assim, a equação da circunferência é:
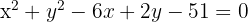
Observação: A outra maneira seria determinar o centro da circunferência  e usar a equação ordinária para encontrar o raio.
e usar a equação ordinária para encontrar o raio.
A representação gráfica da circunferência pode ser vista na figura a seguir.
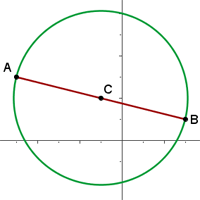
Os extremos do diâmetro de uma circunferência são  e
e  . Qual é a equação dessa circunferência?
. Qual é a equação dessa circunferência?
Para resolver este problema, devemos encontrar o raio e o centro.
O raio é a metade do diâmetro, portanto, será a metade da distância entre  e
e  :
:
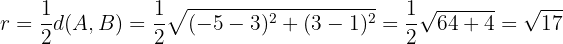
Por outro lado, o centro é o ponto médio entre  e
e  :
:

Dessa forma, a equação ordinária da circunferência é:
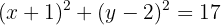
Enquanto a equação geral é:
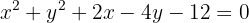
A representação gráfica pode ser vista a seguir.
Encontre a equação da circunferência concêntrica à 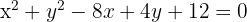 e que passa pelo ponto
e que passa pelo ponto 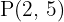 .
.
Para resolver esta equação, precisamos encontrar o centro da circunferência. Portanto, vamos trabalhar com a forma ordinária. O centro é dado por:

Uma vez encontrado o centro, devemos calcular a distância entre o centro e a reta dada; essa distância será o raio:
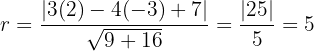
Portanto, a equação da circunferência é:

A representação gráfica pode ser observada na figura a seguir.
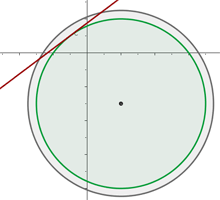
Encontre a equação da circunferência que passa pelos pontos  e
e  , e cujo centro está sobre a reta
, e cujo centro está sobre a reta  .
.
Como precisamos trabalhar com o centro, usaremos a equação reduzida da circunferência, e não a geral.
Seja 
o centro da circunferência e  seu raio.
seu raio.
Sabemos que o centro satisfaz:

Por outro lado, a equação reduzida da circunferência é:
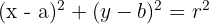
Substituindo o ponto  , temos:
, temos:
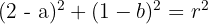
Fazendo o mesmo com o ponto  :
:
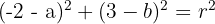
Assim, obtemos o seguinte sistema de equações (não linear):
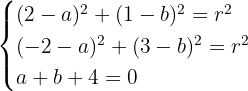
Para resolver, igualamos as duas primeiras equações (já que ambas são iguais a  ) :
) :
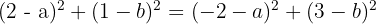
Desenvolvendo os binômios e simplificando, obtemos:
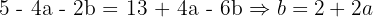
Da terceira equação, isolamos  :
:  .
.
Substituindo essa expressão na anterior:
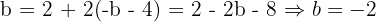
Com isso, 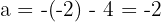 .
.
Substituindo  e
e  na primeira equação do sistema, obtemos:
na primeira equação do sistema, obtemos:
 .
.
Assim, a equação reduzida da circunferência é:
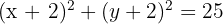
Veja o grafico:
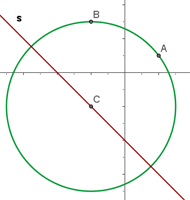
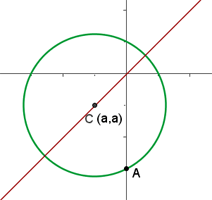
Calcule a equação da circunferência que passa pelo ponto  , tem raio
, tem raio  e centro localizado sobre a bissetriz dos quadrantes primeiro e terceiro.
e centro localizado sobre a bissetriz dos quadrantes primeiro e terceiro.
Sabemos que a bissetriz dos quadrantes primeiro e terceiro é a reta:
 (ou
(ou  ).
).
Isso significa que o centro da circunferência,  , satisfaz a:
, satisfaz a:
 , ou seja,
, ou seja,
podemos escrevê-lo como  .
.
Como a circunferência passa pelo ponto  e tem raio
e tem raio  ,
,
substituímos esses dados na forma reduzida da equação da circunferência:
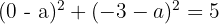
Só temos  como incógnita, então essa equação é suficiente. Desenvolvendo os binômios:
como incógnita, então essa equação é suficiente. Desenvolvendo os binômios:
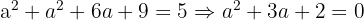
Temos, assim, uma equação do segundo grau. Usando a fórmula de Bhaskara (ou outro método), encontramos:
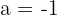 e
e 
Portanto, há duas circunferências que atendem às condições do problema.
A primeira tem centro em  , e sua equação, primeiro na forma reduzida e depois na forma geral, é:
, e sua equação, primeiro na forma reduzida e depois na forma geral, é:
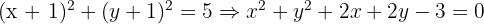
A segunda tem centro em  , e sua equação é:
, e sua equação é:
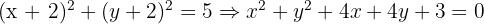
Esse é o gráfico: