Temas
- Calcule o lado que falta do triângulo
- Conhecendo b e c, calcule o a
- Conhecendo um lado e um ângulo, podemos resolver o triângulo
- Resolva o triângulo conhecendo um lado e um ângulo
- Resolva o seguinte triângulo retângulo
- Calcule as informações desconhecidas do seguinte triângulo
- Conhecendo dois lados do triângulo, podemos resolvê-lo
- Resolva o triângulo como indicado
- Problema da árvore e a sombra
- Tendo como base os triângulos anteriores, calcule a distância
- Calcule o raio da circunferência
- Calcule a área sabendo um ângulo e dois lados
- Calcule a altura da árvore
- Calcule os valores dos raios
- Calcule o lado e apótema do octógono
- Encontre a distância entre 2 cidades

Calcule o lado que falta do triângulo
De um triângulo retângulo  , temos a seguinte informação:
, temos a seguinte informação:
A hipotenusa:  .
.
Um dos catetos: 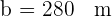
Resolva o triângulo.
De um triângulo retângulo  , temos a seguinte informação:
, temos a seguinte informação:
A hipotenusa:  .
.
Um dos catetos: 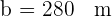
Resolva o triângulo.
Resolver o triângulo significa encontrar as medidas do lado que falta e os valores de todos os ângulos nele. Nota-se que, sendo um triângulo retângulo, sabemos que o ângulo  .
.
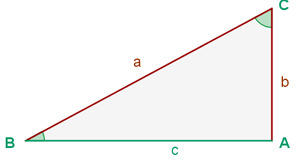
Aplicando o seno temos que
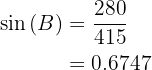
Aplicando o arco seno, temos que o ângulo vale . Agora, uma vez que temos dois ângulos, podemos calcular imediatamente o último;
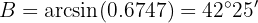
Agora, uma vez que temos dois ângulos, podemos calcular imediatamente o último.:

Aplicando cosseno no ângulo  e resolvendo, vamos obter o valor do lado
e resolvendo, vamos obter o valor do lado :
:
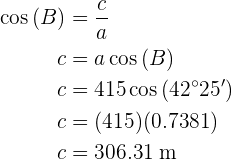
Desta forma, conseguimos obter as informações que faltavam.
Conhecendo b e c, calcule o a
De um triângulo retângulo  , sabemos que os catetos
, sabemos que os catetos
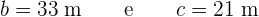
Resolva o triângulo.
De um triângulo retângulo  , sabemos que os catetos
, sabemos que os catetos
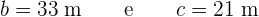
Resolva o triângulo.
"Resolver o triângulo" significa encontrar os lados e ângulos que faltam. É importante notar que, sendo um triângulo retângulo, também sabemos que o ângulo 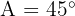 .
.
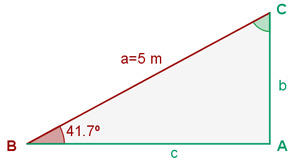
Para encontrar o ângulo  vamos calcular a tangente e em seguida, vamos aplicar a função arco-tangente.:
vamos calcular a tangente e em seguida, vamos aplicar a função arco-tangente.:
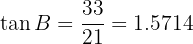
Então, ao aplicarmos a função arco-tangente, 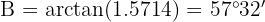 . Desta forma, temos dois ângulos, então podemos calcular diretamente o terceiro.
. Desta forma, temos dois ângulos, então podemos calcular diretamente o terceiro.  :
:
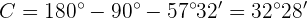
Por último, para obter o valor do lado  vamos utilizar a fórmula do seno e vamos a aplicar ao ângulo
vamos utilizar a fórmula do seno e vamos a aplicar ao ângulo  , então, vamos resolver
, então, vamos resolver  para encontrar seu valor.
para encontrar seu valor.
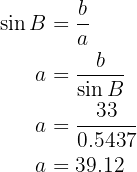
Assim, conseguimos os dados que faltavam.
Conhecendo um lado e um ângulo, podemos resolver o triângulo
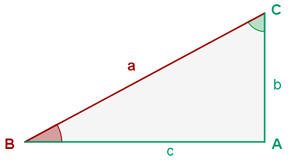
De um triângulo retângulo  , sabe-se a hipotenusa e um dos ângulos, cujos valores são
, sabe-se a hipotenusa e um dos ângulos, cujos valores são

respectivamente. Resolva o triângulo.
De um triângulo retângulo  , sabe-se a hipotenusa e um dos ângulos, cujos valores são
, sabe-se a hipotenusa e um dos ângulos, cujos valores são

respectivamente. Resolva o triângulo.
Resolver um triângulo implica encontrar os lados e ângulos ausentes. Vale notar que, ao ser um ângulo reto, isso implica que  .
.
Ao conhecer dois dos três ângulos, podemos obter o terceiro diretamente.  :
:
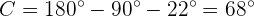
Para obter o lado  vamos aplicar a função seno sobre o ângulo
vamos aplicar a função seno sobre o ângulo  e resolvemos
e resolvemos  :
:
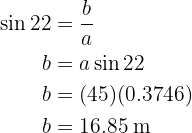
Para obter o lado  aplicamos a função cosseno sobre o ângulo
aplicamos a função cosseno sobre o ângulo  e obtemos
e obtemos  :
:
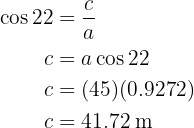
E assim, conseguimos encontrar os dois lados e os ângulos desconhecidos do problema.
Resolva o triângulo conhecendo um lado e um ângulo
De um triângulo retângulo  , conhecemos um cateto e um ângulo
, conhecemos um cateto e um ângulo

Resolva o triângulo.
De um triângulo retângulo  , conhecemos um cateto e um ângulo
, conhecemos um cateto e um ângulo

Resolva o triângulo.
Vamos encontrar os lados e ângulos que faltam. É importante notar que, sendo um ângulo reto, já conhecemos de antemão o ângulo  .
.
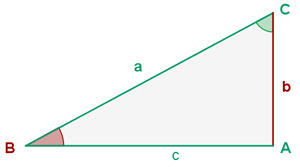
Uma vez que já conhecemos dois dos três ângulos, podemos calcular o que falta. , de maneira direta
, de maneira direta
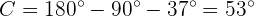
Para obter o lado  aplicamos a função do seno sobre o ângulo.
aplicamos a função do seno sobre o ângulo.  e resolvemos
e resolvemos  :
:
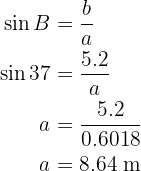
Para obter o lado  Aplicamos a função da cotangente sobre o ângulo.
Aplicamos a função da cotangente sobre o ângulo.  e resolvemos
e resolvemos  :
:
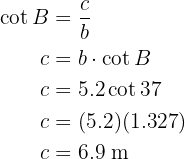
E, assim, encontramos os lados e ângulos que faltavam.
Resolva o seguinte triângulo retângulo
De um triângulo retângulo  , temos a hipotenusa e um ângulo
, temos a hipotenusa e um ângulo

Resolva o triângulo.
De um triângulo retângulo  , temos a hipotenusa e um ângulo
, temos a hipotenusa e um ângulo

Resolva o triângulo.
Vamos determinar os lados e ângulos restantes. É importante observar que, sendo um ângulo reto, já conhecemos o ângulo de antemão.  .
.

Uma vez que já conhecemos dois dos três ângulos, podemos calcular o que falta,  , de maneira direta
, de maneira direta
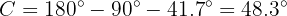
Para obter o lado  aplicamos a função do seno sobre o ângulo
aplicamos a função do seno sobre o ângulo  e resolvemos
e resolvemos  :
:
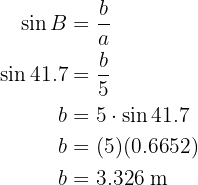
Para obter o lado  aplicamos a função do cosseno sobre o ângulo
aplicamos a função do cosseno sobre o ângulo  e resolvemos
e resolvemos  :
:
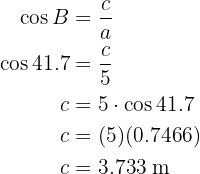
E desta forma, encontramos os lados e ângulos em falta.
Calcule as informações desconhecidas do seguinte triângulo
De um triângulo retângulo  , conhecemos um cateto e um ângulo
, conhecemos um cateto e um ângulo

Resolva o triângulo.
De um triângulo retângulo  , sabemos o cateto e um ângulo
, sabemos o cateto e um ângulo

Resolva o triângulo.
Vamos obter os lados e ângulos desconhecidos. É importante observar que, sendo um ângulo reto, já conhecemos o ângulo de antemão.  .
.
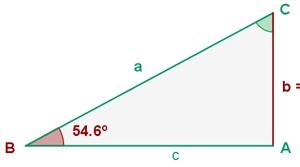
Já que conhecemos dois dos três ângulos, podemos calcular o que está faltando,  , de maneira direta
, de maneira direta
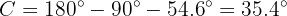
Para obter o lado  aplicamos a função tangente sobre o ângulo
aplicamos a função tangente sobre o ângulo  e resolvemos
e resolvemos  :
:
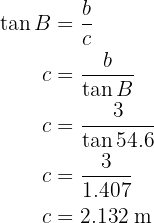
Para obter o lado  aplicamos a função do seno sobre o ângulo
aplicamos a função do seno sobre o ângulo  e resolvemos
e resolvemos  :
:
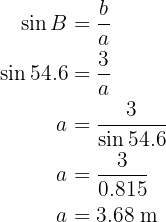
E, desta forma, encontramos os lados e ângulos desconhecidos.
Conhecendo dois lados do triângulo, podemos resolvê-lo
De um triângulo retângulo  , conhecemos a hipotenusa e um dos catetos.
, conhecemos a hipotenusa e um dos catetos.

Resolva o triângulo.
De um triângulo retângulo  , conhecemos a hipotenusa e um dos catetos.
, conhecemos a hipotenusa e um dos catetos.

Resolva o triângulo.
Vamos determinar os lados e ângulos restantes. É importante observar que, sendo um ângulo reto, já conhecemos o ângulo de antemão.  .
.
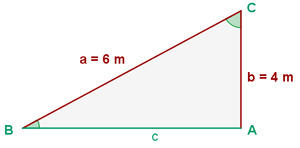
Para obter o ângulo  primeiro calculamos a função cosseno do ângulo utilizando o cateto e a hipotenusa que conhecemos para, então, aplicar a função inversa de arco seno.
primeiro calculamos a função cosseno do ângulo utilizando o cateto e a hipotenusa que conhecemos para, então, aplicar a função inversa de arco seno.
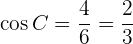
Aplicando arco seno obtenemos  . Notamos que, agora que temos dois de os três ângulos, podemos calcular de forma direta o ângulo que falta
. Notamos que, agora que temos dois de os três ângulos, podemos calcular de forma direta o ângulo que falta

Para obter o lado  aplicamos a função do seno sobre o ângulo
aplicamos a função do seno sobre o ângulo  e resolvemos
e resolvemos  :
:
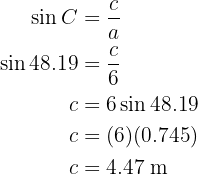
Encontramos os lados e ângulos em falta.
Resolva o triângulo como indicado
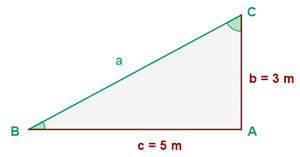
De um triângulo retângulo  , é conhecido os dois catetos
, é conhecido os dois catetos

Resolva o triângulo.
De um triângulo retângulo  , conhecemos os dois catetos
, conhecemos os dois catetos

Resolva o triângulo.
Vamos encontrar os lados e ângulos que faltam. Note que, sendo um ângulo reto, já conhecemos de antemão o ângulo  .
.
Para obter o ângulo  primeiro, vamos calcular a tangente utilizando os catetos e, então, calcular o arco tangente
primeiro, vamos calcular a tangente utilizando os catetos e, então, calcular o arco tangente
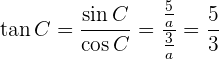
Desta maneira, temos que  . Agora que temos dois dos três ângulos, podemos obter o que está faltando de forma direta
. Agora que temos dois dos três ângulos, podemos obter o que está faltando de forma direta
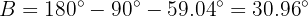
Para obter o lado  aplicamos a função do seno sobre o ângulo
aplicamos a função do seno sobre o ângulo  e resolvemos
e resolvemos  :
:
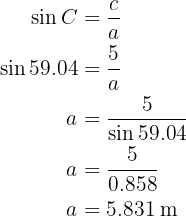
Encontramos os lados e ângulos que faltavam.
Problema da árvore e a sombra
Uma árvore de  de altura projeta uma sombra de
de altura projeta uma sombra de  de largura.
de largura.
Encontre o ângulo de elevação do sol nesse momento.
Uma árvore de  de altura projeta uma sombra de
de altura projeta uma sombra de  de largura.
de largura.
Encontre o ângulo de elevação do sol nesse momento.
Observe que entre o solo e a árvore se forma um ângulo de  . Dessa forma, temos dois catetos. Além do mais, temos que o ângulo de elevação é o ângulo formado no vértice onde termina a sombra como é possível observar na imagem a seguir:
. Dessa forma, temos dois catetos. Além do mais, temos que o ângulo de elevação é o ângulo formado no vértice onde termina a sombra como é possível observar na imagem a seguir:
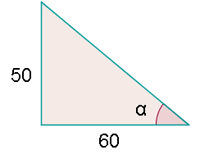
Portanto, para obter o ângulo de elevação  primeiro calculamos a tangente utilizando os catetos e então aplicamos a função arco tangente ao resultado
primeiro calculamos a tangente utilizando os catetos e então aplicamos a função arco tangente ao resultado
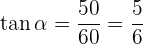
Portanto, temos que  .
.
Tendo como base os triângulos anteriores, calcule a distância
Um balão que está voando 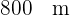 de altura, consegue ver uma cidade com um ângulo de depressão de
de altura, consegue ver uma cidade com um ângulo de depressão de 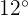 .
.
A que distância da cidade se encontra?
Um balão que está voando a 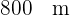 de altura, consegue ver uma cidade com um ângulo de depressão de
de altura, consegue ver uma cidade com um ângulo de depressão de 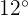 .
.
A que distância da cidade está?
A seguinte imagem mostra o esquema fornecido pelos dados.
Um balão que está voando a 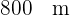 de altura, consegue ver uma cidade com um ângulo de depressão de
de altura, consegue ver uma cidade com um ângulo de depressão de 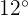 .
.
A que distância da cidade está?
A seguinte imagem mostra o esquema fornecido pelos dados.
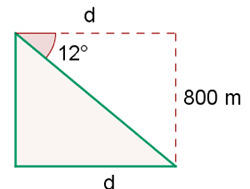
O que realmente queremos é encontrar a distância que o dirigível deve percorrer voando sobre o povoado. Isto é, queremos encontrar o cateto  , para isso, vamos calcular a função da tangente do ângulo com valor
, para isso, vamos calcular a função da tangente do ângulo com valor 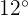 e, ao mesmo tempo, usamos os catetos e então resolvemos,
e, ao mesmo tempo, usamos os catetos e então resolvemos,  :
:
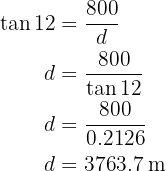
Calcule o raio da circunferência
Encontre o raio de uma circunferência sabendo que uma corda de  tem como arco correspondente de
tem como arco correspondente de  .
.
Encontre o raio de uma circunferência sabendo que uma corda de  tem como arco correspondente de
tem como arco correspondente de  .
.
Vamos lembrar que o ângulo central tem a mesma medida que o arco que ele abrange. Dito isso, temos o seguinte esquema.
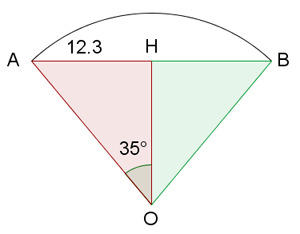
Para obter o raio (lado 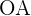 ) vamos aplicar a função do seno sobre o ângulo que mede
) vamos aplicar a função do seno sobre o ângulo que mede  utilizando o cateto que conhecemos e
utilizando o cateto que conhecemos e 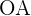 e então resolver o raio:
e então resolver o raio:
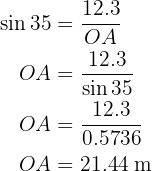
Calcule a área sabendo um ângulo e dois lados
Calcule a área de um terreno triangular, sabendo que dois dos seus lados medem 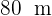 e
e 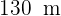 , e formam entre si um ângulo de
, e formam entre si um ângulo de  .
.
Calcule a área de um terreno triangular, sabendo que dois de seus lados medem 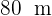 e
e 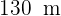 , e formam entre si um ângulo de
, e formam entre si um ângulo de  .
.
Vamos encontrar o ângulo 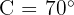 . Agora, na seguinte imagem mostramos o triângulo.
. Agora, na seguinte imagem mostramos o triângulo.
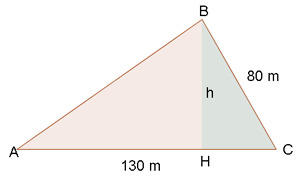
Perceba que a altura divide nosso triângulo inicial em dois triângulos retângulos. Vamos utilizar o triângulo da direita, pois temos mais informações nele, para obter o valor da altura e, posteriormente, calcular a área. Para encontrar a altura, vamos usar o seno do ângulo.  , o cateto que pertence este triângulo e a altura, assim, terminamos resolvendo a altura:
, o cateto que pertence este triângulo e a altura, assim, terminamos resolvendo a altura:
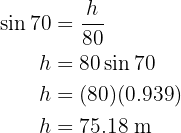
Agora que sabemos que a altura mede 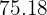 , vamos calcular a área:
, vamos calcular a área:
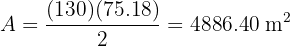
Calcule a altura da árvore
Calcule a altura de uma árvore, sabendo que a partir de um ponto do terreno sua copa é observada sob um ângulo de  e, ao aproximar
e, ao aproximar  , sob um ângulo de
, sob um ângulo de 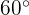 .
.
Calcule a altura de uma árvore, sabendo que a partir de um ponto do terreno sua copa é observada sob um ângulo de  e, ao aproximar
e, ao aproximar  , sob um ângulo de
, sob um ângulo de 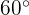 .
.
Vamos tentar ilustrar o problema para entender melhor. A seguinte imagem nos ajudará com isso.
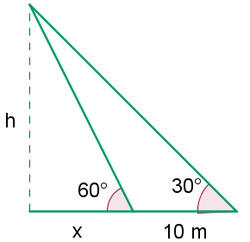
Para resolver o problema, primeiro calculamos a tangente do ângulo de  e os catetos correspondentes e então, calculamos a tangente do ângulo de
e os catetos correspondentes e então, calculamos a tangente do ângulo de 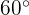 com os catetos correspondentes e resolvemos
com os catetos correspondentes e resolvemos  de ambos:
de ambos:
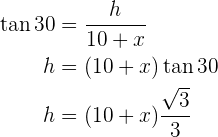
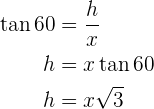
É importante destacar que isso nos dará um sistema de equações para solucionar a altura
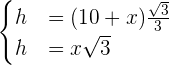
Resolvendo o sistema temos que 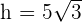 .
.
Calcule os valores dos raios
O comprimento do lado de um octógono regular é  . Encontre os raios da circunferência inscrita e circunscrita.
. Encontre os raios da circunferência inscrita e circunscrita.
O comprimento do lado de um octógono regular é  . Encontrar os raios da circunferência inscrita e circunscrita.
. Encontrar os raios da circunferência inscrita e circunscrita.
A próxima imagem nos permite observar qual é o raio da circunferência inscrita e qual é o da circunferência circunscrita.
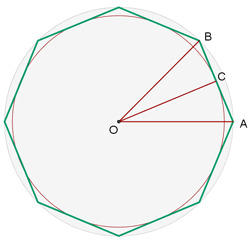
Note que o lado  . Além disso, o lado
. Além disso, o lado 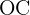 define o raio da circunferência inscrita, enquanto que o lado
define o raio da circunferência inscrita, enquanto que o lado 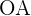 define o raio da circunferência circunscrita. Ainda, sabemos que o ângulo
define o raio da circunferência circunscrita. Ainda, sabemos que o ângulo  já que se trata de um octógono, portanto, temos que
já que se trata de um octógono, portanto, temos que  .
.
Raio da circunferência inscrita
Calculamos a tangente do ângulo 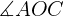 utilizando tanto o valor do ângulo como os catetos para, no final, poder resolver o cateto
utilizando tanto o valor do ângulo como os catetos para, no final, poder resolver o cateto  .
.
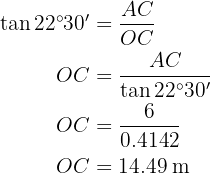
Raio da circunferência circunscrita
Calculamos o seno do ângulo  utilizando tanto o valor do ângulo como o cateto e a hipotenusa para, no final, poder resolver a hipotenusa
utilizando tanto o valor do ângulo como o cateto e a hipotenusa para, no final, poder resolver a hipotenusa  .
.
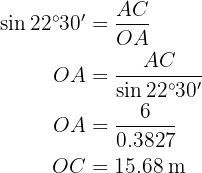
Calcule o lado e apótema do octógono
Calcule o comprimento do lado e a apótema de um octógono regular inscrito em uma circunferência de 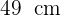 de raio.
de raio.
Calcule o comprimento do lado e a apótema de um octógono regular inscrito em uma circunferência de 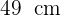 de raio.
de raio.
A imagem abaixo nos permite observar melhor o problema.
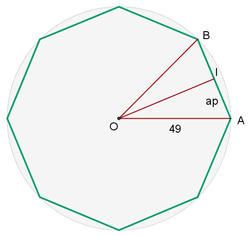
Observe que el raio é igual ao lado 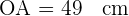 . Assim, o lado do octógono está definido por
. Assim, o lado do octógono está definido por  e que
e que 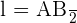 .
.
Também notamos que o apótema 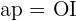 separa o ângulo
separa o ângulo  em dois. Além disso, sabemos que o ângulo
em dois. Além disso, sabemos que o ângulo  já que se trata de um octógono, portanto, temos que
já que se trata de um octógono, portanto, temos que 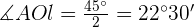 . Vamos notar, também, que os lados
. Vamos notar, também, que os lados 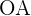 ,
,  e
e 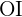 formam um triângulo retângulo.
formam um triângulo retângulo.
Lado do octógono
Vamos calcular o seno do ângulo 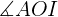 utilizando tanto o valor do ângulo como a hipotenusa (o raio do octógono) e o cateto (a metade de um lado do octógono) para, no final, poder resolver o cateto
utilizando tanto o valor do ângulo como a hipotenusa (o raio do octógono) e o cateto (a metade de um lado do octógono) para, no final, poder resolver o cateto  .
.
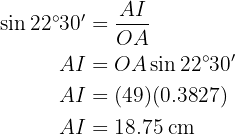
Portanto, o lado mede 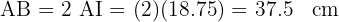 .
.
Apótema do octógono
Vamos calcular o cosseno do ângulo 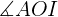 utilizando tanto o valor do ângulo como o da hipotenusa (o raio do octógono) e o cateto (a apótema) para, no final, poder resolver o cateto
utilizando tanto o valor do ângulo como o da hipotenusa (o raio do octógono) e o cateto (a apótema) para, no final, poder resolver o cateto 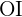 .
.
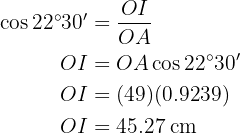
Encontre a distância entre 2 cidades
Três cidades  ,
,  e
e  estão unidas por estradas. A distância de
estão unidas por estradas. A distância de  a
a  é de
é de 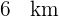 e a de
e a de  a
a  de
de 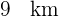 . Além disso, o ângulo que formam entre as estradas é de
. Além disso, o ângulo que formam entre as estradas é de 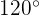 .
.
Qual a distância entre  e
e  ?
?
Três cidades  ,
,  e
e  estão unidas por estradas. A distância de
estão unidas por estradas. A distância de  a
a  é de
é de 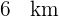 e a de
e a de  a
a  de
de 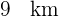 . Além disso, o ângulo que formam entre as estradas é de de
. Além disso, o ângulo que formam entre as estradas é de de 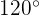 .
.
Qual a distância entre  e
e  ?
?
A seguinte imagem nos ajudará a observar melhor o problema.
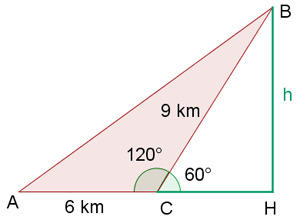
Perceba que fizemos algumas construções adicionais para resolver o problema usando triângulos retângulos. Para resolver o problema, primeiro precisamos encontrar os catetos do triângulo retângulo que formamos (o de cor verde) e, posteriormente, usaremos esses dados para obter os catetos do triângulo maior e, assim, a hipotenusa, que é o valor que estamos procurando.
Catetos do triângulo retângulo verde
Calculamos seno e o cosseno do ângulo 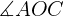 utilizando tanto o valor do ângulo como os catetos e a hipotenusa para, no final, poder resolver los catetos
utilizando tanto o valor do ângulo como os catetos e a hipotenusa para, no final, poder resolver los catetos  e
e  , respectivamente.
, respectivamente.

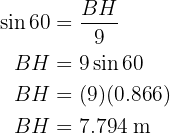
Catetos do triângulo retângulo maior e hipotenusa
Utilizamos o teorema de Pitágoras para calcular a hipotenusa. Primeiro, temos que os catetos que utilizamos são  e
e 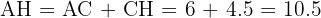 .
.

Resumir com IA:












